Neural audio codecs or tokenizers

• https://kyutai.org/codec-explainer

• We’ll have a look at why audio is harder to model than text and how we can make it easier with neural audio codecs, the de-facto standard way of getting audio into and out of LLMs.

• With a codec, we can turn audio into larger discrete tokens, train models to predict continuations for these tokens, and then decode those back into audio

Baseline

• What’s the most basic model we can train to generate audio?
  • Baseline model that generates audio sample by sample
  • Similar to a character language model
  • The input and outputs will be, like in Wavenet, 256 discrete buckets, obtained by the mu-law algorithm to quantize the real-valued signal into buckets.
  • For the dataset, we’ll use the Libri-Light dataset, following AudioLM i.e. next-token prediction unsupervised learning.
  • context length is 2048. which, for 16 kHz audio, translates to 128ms, not even the length of one word. Also, 10-second examples took 30 minutes to generate on an H100, so we’re a few orders of magnitude away from being real-time.
  • We need a neural audio codec to compress the audio. The hope is that if we reduce the sampling rate 100x, the model will also become “100x more coherent”.

VQ-VAE

• Already covered in VQ-VAE
• Main thing to remember is:
  • we have an encoder that maps the input into a latent space
  • within that latent space, we define $K$ embeddings or “clusters” that define the “tokens” or “buckets”
  • we have an decoder that takes in one of the $K$ embeddings and reconstructs the input

The code looks like this:

x = get_batch()
z = encoder(x)
 
residual = z - to_nearest_cluster(z)
# .detach() means "forget that this needs a gradient"
# ste-estimator
z_quantized = z - residual.detach()
x_reconstructed = decoder(z_quantized)
 
loss = reconstruction_loss(x, x_reconstructed)

Residual vector quantization

• In the VQ-VAE setting, to improve the reconstruction fidelity, we need increase the number of cluster centers.

  • But keeping track of too many centers can get prohibitively expensive, as the embedding table blows up.

• So we’ll do a clever trick: if we want $2^{20}$ (~1M) possible values, we won’t create $2^{20}$ clusters directly.

  • Instead, we’ll use two separate quantizers with $2^{10}=1024$ clusters and combine their result. Each embedding will then be quantized to a tuple of two integers in $[\mathrm{0..1023}]$, yielding $2^{20}$ possible combinations.

• How?

  • Recall the residual variable we used in the straight-through estimator, defined as z - to_nearest_cluster(z) the shift from the quantized embedding to the unquantized one.
  • It represents the part of the original vector z that we didn’t manage to take into account when quantizing to to_nearest_cluster(z).
  • The solution is obvious: we’ll quantize these residuals exactly the same way we did with the original embeddings, by training another vector quantizer.

• The residual vector quantization algorithm

def rvq_quantize(z):
    residual = z
    codes = []
 
    for level in range(levels):
        quantized, cluster_i = to_nearest_cluster(level, residual)
        residual -= quantized
        codes.append(cluster_i)
 
    return codes

Residual vector quantization was first applied to neural audio codecs in SoundStream, but the idea has been around since the 80s.

Tokenizing audio with a neural audio codec

Architecture

• We’ll use RVQ on audio.
• As our autoencoder, we just need a sequence processing architecture capable of downsampling.
  • we can use a convolutional neural network (CNN) similar to what Jukebox uses i.e. it’s a bunch of conv1d layers, processing a sequence of real values.
  • What’s important is that it’s a network that takes an audio with t samples and converts it to a vector of shape (T / P, D).
    • In other words, it downsamples by a factor of 128 and gives us 32-dimensional float representations.
      • This is similar to patching for images
    • The decoder then takes the (T/P, D) embeddings and decodes them back into t samples.

audio = get_batch()                         # [B, T]
z = encoder(audio)                          # [B, T/P, D]
 
# Combine the batch and time dimensions
z = rearrange(                              # [B*T/P, D]
    z, "b t_emb d -> (b t_emb) d"
)
 
codes = rvq_quantize(z)           # integers, [B*T/P, levels]
z_quantized = codes_to_embeddings(codes)    # [B*T/P, D] ## can be concatenation or summation.
z_quantized = rearrange(                    # [B, T/P,D]
    z_quantized, "(b t_emb) d -> b t_emb d"
)
 
audio_reconstructed = decoder(z_quantized)  # [B, T]

Loss function

• The last missing piece before we can train our first neural audio codec is a loss function.
• There’s a whole rabbit hole we could go into about which one to choose, but we’ll avoid it (more details here) and just use a very simple one.
• We can compute the log amplitude spectrogram of the original and reconstructed audio, and take their difference. The loss is the mean square of this difference between spectrograms.
  • 
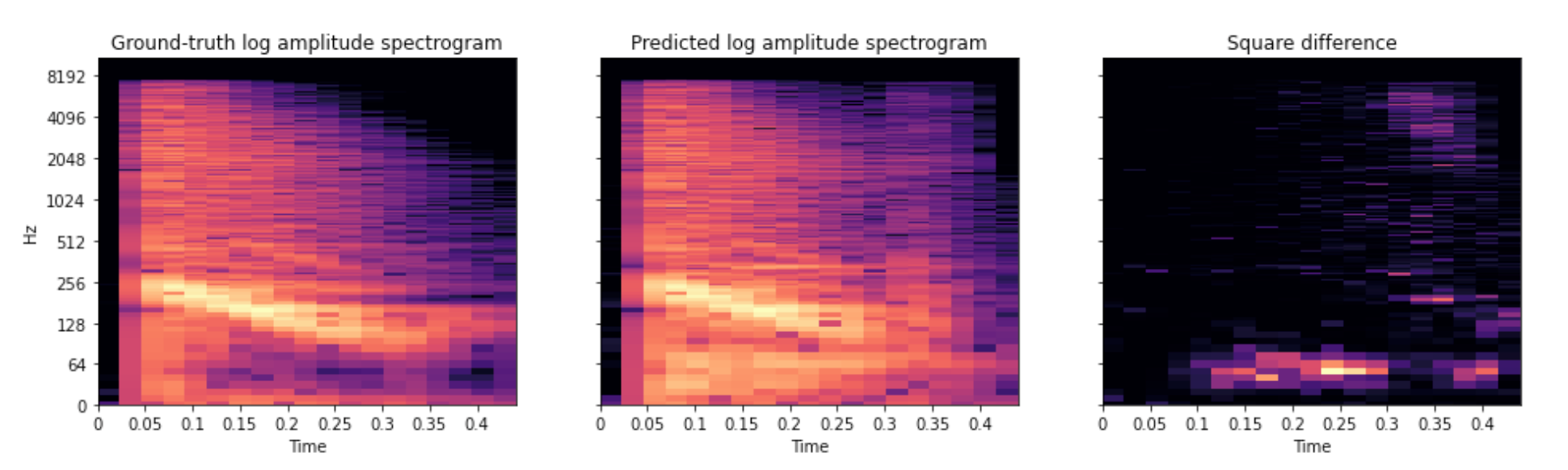
  • To make it harder for the model to overfit to this loss, we take the spectrogram with three different parameters for the short-time Fourier transform, and let our loss be the mean between the three sub-losses. This is called the multi-scale spectral loss
• The best loss is an adversarial loss, like a GAN

How to input and output a multi-level RVQ to a token-based model?

• When using an RVQ, we have this step:

z = encoder(audio)                          # [B, T/P, D]
# Combine the batch and time dimensions
z = rearrange(                              # [B*T/P, D]
    z, "b t_emb d -> (b t_emb) d"
)
codes = rvq_quantize(z)           # integers, [B*T/P, levels]
z_quantized = codes_to_embeddings(codes)   # [B, S, emb_dim]

• code_to_embeddings can be defined however we want.
• Let’s assume that P=128 and levels=8
• This means that for each time step, we actually have eight tokens instead of one like in text.
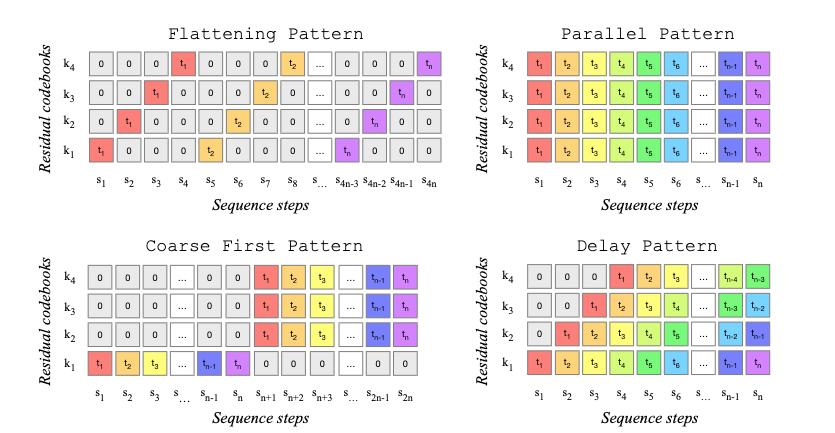
• The simplest approach is to flatten the array into (B, T/P*levels, D)
  • The big disadvantage is that we lose some temporal compression, which can be expensive with transformer models
  • By default, this also means we need to predict the eight levels in separate time steps, i.e. auto-regressively.

Multi-level RVQ sampling

• You could also predict all RVQ levels for a single step at once (”parallel pattern”), but it also makes things harder for the model because it has to decide on all levels at once.

• There are a bunch of other schemes people have tried to balance compression and quality. Here are a few tried out in MusicGen

• . In RVQ, each quantizer encodes the quantization error left by the previous quantizer, thus quantized values for different codebooks are in general not independent, and the first codebook is the most important one.

• This affects both training and inference

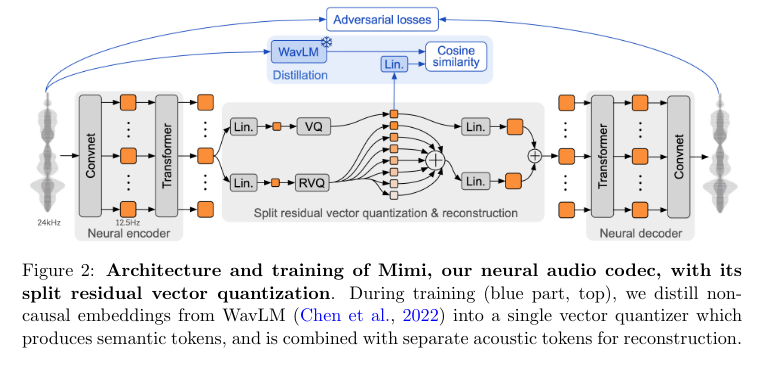
Mimi, kyutai neural audio codec