Thoughts on verification

Sources:

• https://www.youtube.com/watch?v=nXQE1DsPm2c

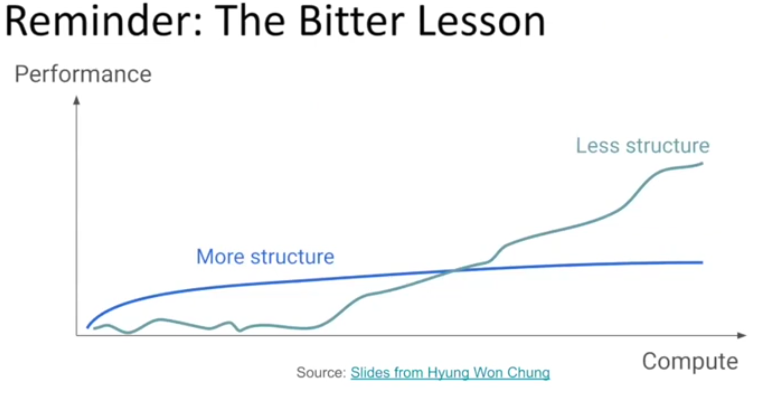
• Scaling RL compute for LLMs on any domain is bottlenecked by how “good” verified we have.

⇒ how do we build powerful LLM verifiers that scale with computation?

• Classic discriminative classifiers predict a scalar score using a linear layer on top of LLMs

  • They do not use the text generation capabilities of LLMs
  • Cannot leverage “test-time compute” to improve performance

• Generative verifiers can

  • use reasoning
  • parallel sampling ⇒ average or majority voting

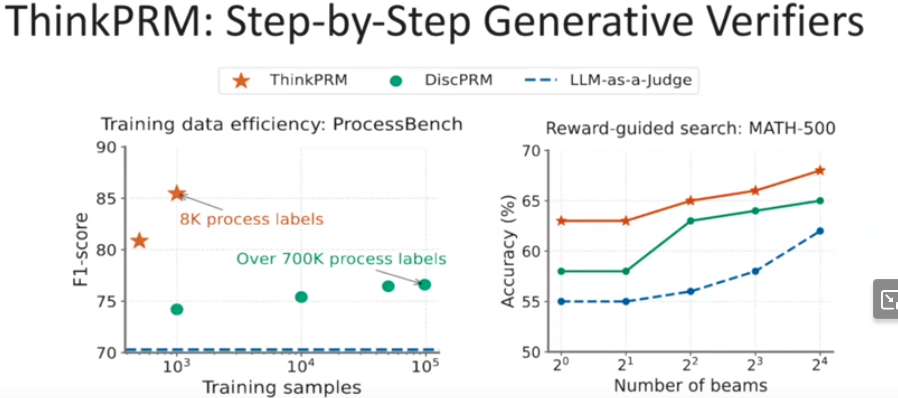
• Training generative verifiers, for a given domain, is more data efficient than training classifiers (about 100x for math domains)

  • 

Self-Verification: Unifying LLM Reasoners with Generative Verifiers

• https://arxiv.org/abs/2505.04842
• The same model does the generation and verification
• They train the model both with an RL loss (for generation) and an SFT loss (for verification)
• Then, at test time, you can use the model to assign a ranking to its own solutions
• 
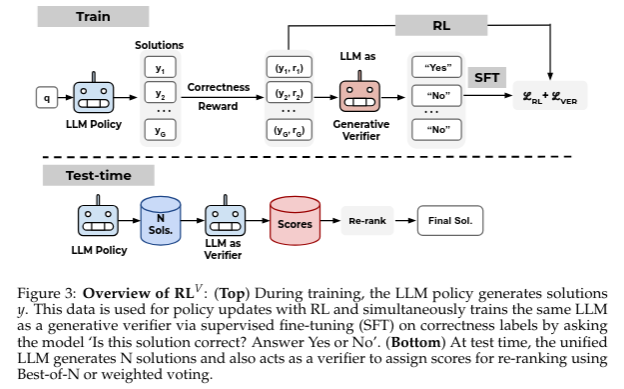
• Prevalent reinforcement learning~(RL) methods for fine-tuning LLM reasoners, such as GRPO , abandon the learned value function in favor of empirically estimated returns.
  • This hinders test-time compute scaling that relies on using the value-function for verification. In this work, they propose RLV that augments any ‘value-free’ RL method by jointly training the LLM as both a reasoner and a generative verifier using RL-generated data, adding verification capabilities without significant overhead.
  • Empirically, RLV boosts MATH accuracy by over 20% with parallel sampling and enables 8−32× efficient test-time compute scaling compared to the base RL method.
  • RLV also exhibits strong generalization capabilities for both easy-to-hard and out-of-domain tasks.