NVFP4 format

Reminder of the floating point encoding

Encoding

• $S$ = sign bit, $E$ = exponent bits, $M$= fraction or mantissa bits
• Value = $(-1{)}^S\times 2^{E-\text{exponent bias}}\times (1.M)$ (in most cases, special values apply e.g. zero and infinity)
• exponent bias = $2^{\text{num\_bits}(E)-1}-1$ (maximum positive value) e.g. 127 with 8 exponent bits

MX formats

• Due to the limited range of narrow floating-point formats, microscaling (MX) formats were introduced to balance dynamic range and precision.
• These formats are characterized by a block-wise representation where a group of data elements shares a single, common scale factor.
• MX formats include 8-bit (MXFP8), 6-bit (MXFP6), and 4-bit (MXFP4) floating-point types.
• In MXFP4, each element is represented as E2M1, meaning it has 1 sign bit, 2 exponent bits, and 1 mantissa bit.
• This allows MXFP4 to encode the values ±0, ±0.5, ±1, ±1.5, ±2, ±3, ±4, and ±6

MXFP4

• TLDR; group size = 32, 8 bit scales in (UE8M0)

• Since original higher-precision values (e.g., FP32 or BF16) often exceed the FP4 range, they must be scaled into the representable range during quantization.

• Scale factors are typically chosen so that the absolute maximum value (amax) within a block maps to the FP4 maximum representable,

• . After scaling, high precision values in a tensor are rounded to the nearest FP4-representable number and later decoded back to their original range using the reciprocal of the same scale.

• To improve hardware efficiency, MX formats store block scale factors in 8 bits.

• Each block of 32 contiguous elements in a tensor shares a single 8-bit scale factor, stored in an unsigned E8M0 format (UE8M0), which encodes a power-of-two value ranging from $2^{-127}$ to $2^{127}$.

NVFP4

• TLDR; group size = 16. Hierarchical scaling ⇒ 8 bit scales in E4M3 at the group level, FP32 scales at the tensor level.

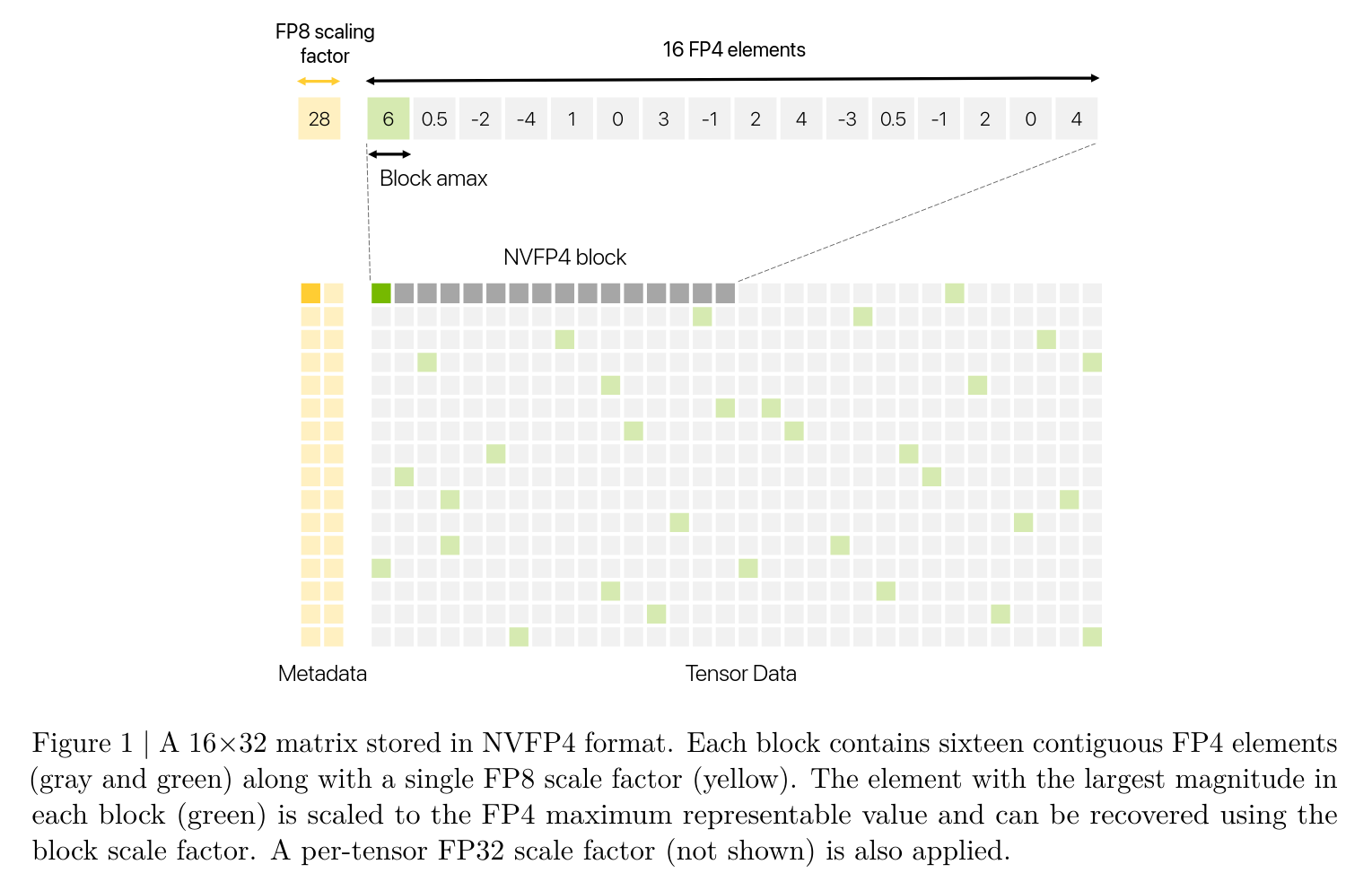
• NVFP4 is an enhanced 4-bit format that provides improved numerical properties over MXFP4.

• First, by reducing the block size from 32 to 16 elements, NVFP4 narrows the dynamic range within each block, better fitting values into the FP4 range.

• Second, block scale factors are stored in E4M3 rather than UE8M0, trading some exponent range for additional mantissa bits.

• Third, an FP32 scale is applied at the tensor level to retain the range of block scales.

• With such a two-level microscaling approach, NVFP4 encodes at least 6.25% of values in a block (the amax values in each block of 16 elements) at near-FP8 precision, while storing the remaining values in FP4.

• In contrast, MXFP4 stores all values in FP4, and can potentially lose up to one binade of dynamic range (and four samples: ±4 and ±6) because of power-of-two scale factor rounding (see Appendix B.4 for details)

Implementation

You choose the FP32 scale so that all per-block “ideal” scales (the ones you’d need to fit values into FP4) fit cleanly into the numeric range of E4M3 and keep good precision. In practice:

• Let $a_{\max }^{(b)}={\max }_{i\in b}|x_i|$ for each 16-elem block $b$.
• FP4(E2M1) tops out at about 6 in magnitude, and E4M3 covers roughly $[-448,448]$.
• Because we have the double layering of scales, the effective range that the “quantized values” can take is $[-6\ast 448,6\ast 448]$

1. Pick a global FP32 scale $s_g\approx {\max }_b{a}_{\max }^{(b)}/(6\cdot 448)$. (to cover the range we expect out of the first layer of quantization)

2. Then each FP8 block scale is $s_b=cast\_E4M3((a_{\max }^{(b)}/s_g)/6)$

   • first we scale the tensor amax within the range $[-6\ast 448,6\ast 448]$ using the fp32 scale
   • then we scale the blockwise scale itself within FP8

3. Quantize each value as $q_i=cast\_FP4(x_i/(s_g\cdot s_b))$.

   1. This can be seen as (1) dequantize the blockscale itself (2) use the dequantized scale to quantize the block

• Dequant is ${\hat{x}}_i=s_g\cdot s_b\cdot deq\_FP4(q_i)$.
  • First dequant the block scale, then dequant the block