Finite scalar quantization (FSQ) - VQ-VAE Made Simple

• https://arxiv.org/abs/2309.15505

• Improvements over VQ-VAE
  • no aux losses
  • full codebook utilization
  • faster because bottleneck dimension $d$ is usually smaller.

Summary of VQ-VAE

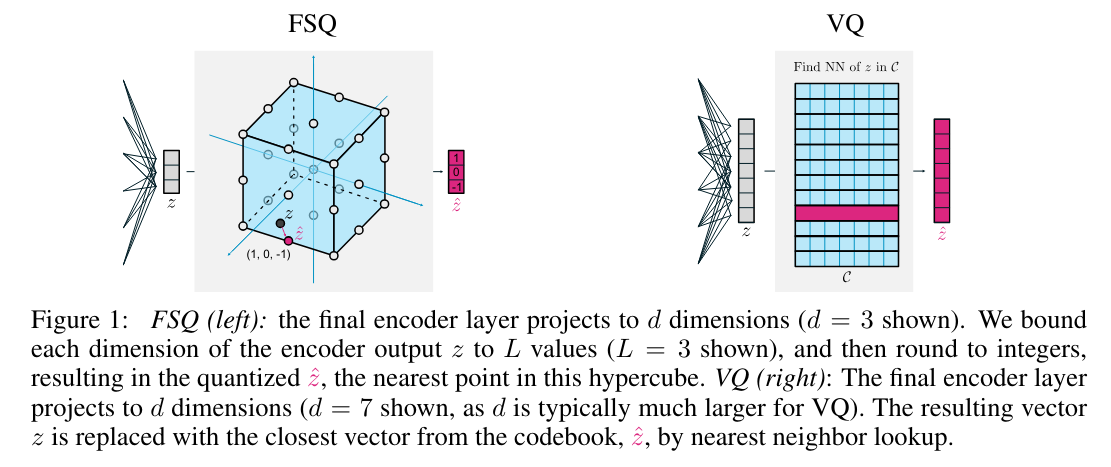
• When training VQ-VAE, the goal is to learn a codebook $C$ whose elements induce a compressed, semantic representation of the input data (typically images). In the forward pass, an image $x$ is encoded into a representation $z$ (typically a sequence of feature vectors), and each vector in $z$ quantized to (i.e., replaced with) the closest vector in $C$.
  • The quantization operation is not differentiable. When training a VAE with VQ in the latent representation, Van Den Oord et al. (2017) use the straight- through estimator (STE) (Bengio et al., 2013), copying the gradients from the decoder input to the encoder output, resulting in gradients to the encoder. Since this still does not produce gradients for the codebook vectors, they further introduce two auxiliary losses to pull the codeword vectors towards the (unquantized) representation vectors and vice-versa.
  • The above formulation is challenging to optimize, and leads to the well-documented problem of underutilized codebooks as the size of $C$ is increased, many codewords will be unused.

FSQ

• The goal of FSQ is simplifying the original VQ-VAE formulation with the following goals:

  • i) remove auxiliary losses,
  • ii) achieve high codebook utilization by design
  • iii) keep the functional setup the same to the extent that we obtain a drop-in replacement for VQ.

• Consider a vector $z$ with $d$ channels. If we map each entry $z_i$ to $L$ values (e.g., via $z_i\to \lfloor L/2\rfloor tanh(z_i)$ followed by rounding to integers), we obtain a quantized $\hat{z}$, where $\hat{z}$ is one of $L^d$ unique possible vectors. The first figure shows FSQ for $d=3,L=3$, implying a codebook $C=(-1,-1,-1),(-1,-1,0),(-1,-1,1),...,(1,1,1)$, where $|C|=L^d=27$.

The important insight is that by carefully choosing how to bound each channel, we can get an implicit codebook of (almost) any desired size.

• To get gradients through the rounding operation, they use the STE like VQ-VAE.
  • Thus, using FSQ inside an autoencoder trained with a reconstruction loss, we get gradients to the encoder that force the model to spread the information into multiple quantization bins, as that reduces the reconstruction loss.
  • As a result, we obtain a quantizer that uses all codewords without any auxiliary losses.