Shortcut & Consistency models

Abstract

• Support fast one-step generation by design, while still allowing multistep sampling to trade compute for sample quality
• trained either by distilling pre-trained diffusion models, or as standalone generative models altogether
• They build on top of the probability flow (PF) ordinary differential equation (ODE) in continuous-time diffusion models, whose trajectories smoothly transition the data distribution into a tractable noise distribution. We propose to learn a model that maps any point at any time step to the trajectory’s starting point.
  • self-consistency property: Points on the same trajectory map to the same initial point
  • 

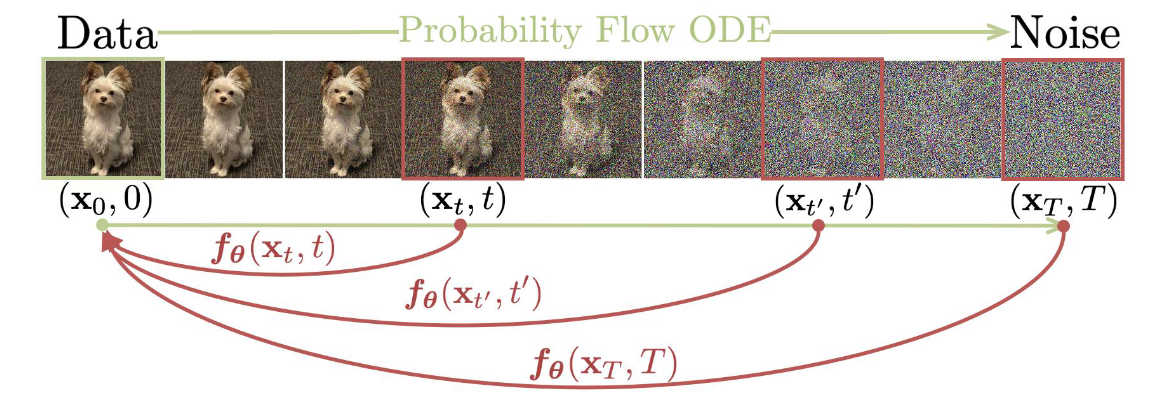
Main idea

• A trained diffusion model, one way or another, estimates the score function of the probability distribution
  • whether that’s done directly through score matching
  • or through denoising objective, where in practice, $\nabla p(x_t)=-\alpha {ϵ}_0$
    • where ${ϵ}_0$ is the source noise i.e. $x_t=x_0+{ϵ}_0$
• As soon as you have the score function, assuming it’s a Gaussian Diffusion model, you can sample trajectories from pure noise $x_T$ to new “clean” samples ${\hat{x}}_0$, using an ODE solver (e.g. Euler).
• Then you can enforce the objective that any samples on a trajectory should be mapped back to ${\hat{x}}_0$.

Shortcut models

• Building on top of the Flow matching training objective, one can define a shortcut model

• Shortcut models condition the neural network not only on the signal level $\tau$ but also on the requested step size $d$.

• This allows them to choose the step size at inference time and generate data points using only a few sampling steps and forward passes of the neural network.

• For the finest step size $d_{\min }$, shortcut models are trained using the flow matching loss. For larger step sizes $d_{\min }<d\le 1$, shortcut models are trained using a bootstrap loss that distills two smaller steps (defined as the average of the two midpoints), where $\mathrm{sg}(\cdot )$ stops the gradient:

$$x_0\sim \mathcal{N}(0,I)x_1\sim \mathcal{D}\tau ,d\sim p(\tau ,d)$$ $$b^{\prime }=f_{\theta }(x_{\tau },\tau ,d/2)b^{\prime \prime }=f_{\theta }(x^{\prime },\tau +d/2,d/2)x^{\prime }=x_{\tau }+b^{\prime }d/2$$ $$\mathcal{L}(\theta )=\Vert f_{\theta }(x_{\tau },\tau ,d)-v_{\text{target}}{\Vert }^2{v}_{\text{target}}=\{\begin{array}{ll}{x}_1-x_0& \text{if }d=d_{\min }\\ \mathrm{sg}(b^{\prime }+b^{\prime \prime })/2& \text{else}\end{array}$$

• The step size is sampled uniformly as a power of two, based on the maximum number of sampling steps $K_{\max }$, which defines the finest step size $d_{\min }=1/K_{\max }$.
• The signal level is sampled uniformly over the grid that is reached by the current step size:

$$d\sim 1/\mathcal{U}(\{1,2,4,8,\dots ,K_{\max }\})\tau \sim \mathcal{U}(\{0,1/d,\dots ,1-1/d\})$$

• At inference time, one can condition the model on a step size $d=1/K$ to target $K$ sampling steps, without suffering from discretization error because the model has learned to predict the end point of each step.
• In practice, shortcut models generate high-quality samples with 2 or 4 sampling steps, compared to 64 or more steps for typical diffusion models.