Multi-Head Latent Attention (MLA)

• Introduced in DeepSeek v2, https://arxiv.org/pdf/2405.04434

• pytorch implementation https://github.com/fla-org/flash-linear-attention/blob/main/fla/layers/mla.py

  • https://github.com/deepseek-ai/DeepSeek-V3/blob/main/inference/model.py#L396

• MLA utilizes low-rank key-value joint compression to eliminate the bottleneck of inference-time key-value cache.

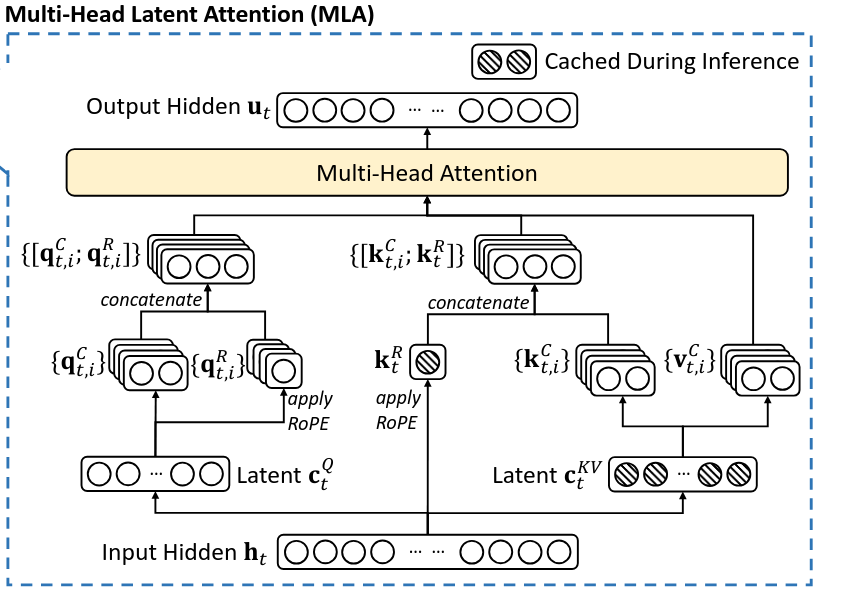
Full Formula of MLA

• Notation:
  • $W^{D\ast }$ is an down-projection matrix to the compressed space
  • $W^{U\ast }$ is an up-projection matrix from the compressed space

Setup and dimensions

Let

• $d_{\text{model}}$ = hidden_dim
• $n_h$ = num_attention_heads
• $d_c$ = qk_nope_head_dim (no-PE/low-rank per-head dim)
• $d_r$ = qk_rope_head_dim (RoPE per-head dim)
• $r_q$ = q_lora_rank
• $r_{kv}$ = kv_lora_rank

Vectors (columns):

• ${\mathbf{h}}_t\in {\mathbb{R}}^{d_{\text{model}}}$
• ${\mathbf{c}}_t^Q\in {\mathbb{R}}^{r_q}$, ${\mathbf{c}}_t^{KV}\in {\mathbb{R}}^{r_{kv}}$
• Per head $i$: ${\mathbf{q}}_{t,i}^C\in {\mathbb{R}}^{d_c}$, ${\mathbf{q}}_{t,i}^R\in {\mathbb{R}}^{d_r}$, ${\mathbf{k}}_{j,i}^C\in {\mathbb{R}}^{d_c}$, ${\mathbf{k}}_j^R\in {\mathbb{R}}^{d_r}$, ${\mathbf{v}}_{j,i}^C\in {\mathbb{R}}^{d_c}$

Matrices (biases omitted; matrices left-multiply column vectors):

• $W^{DQ}\in {\mathbb{R}}^{r_q\times d_{\text{model}}}$ (code: q_down_lora)
• $W^{UQ}\in {\mathbb{R}}^{(n_h{d}_c)\times r_q}$ (code: q_up_nope)
• $W^{QR}\in {\mathbb{R}}^{(n_h{d}_r)\times r_q}$ (code: q_up_rope)
• $W^{DKV}\in {\mathbb{R}}^{r_{kv}\times d_{\text{model}}}$ (code: kv_down_lora)
• $W^{UK}\in {\mathbb{R}}^{(n_h{d}_c)\times r_{kv}}$ (code: k_up_nope)
• $W^{KR}\in {\mathbb{R}}^{(n_h{d}_r)\times d_{\text{model}}}$ (code: k_rope)
• $W^{UV}\in {\mathbb{R}}^{(n_h{d}_c)\times r_{kv}}$ (code: v_up)
• $W^O\in {\mathbb{R}}^{d_{\text{model}}\times (n_h{d}_c)}$ (code: out_proj)

RoPE preserves size: $\mathrm{RoPE}(\cdot ):{\mathbb{R}}^{n_h{d}_r}\to {\mathbb{R}}^{n_h{d}_r}$.

Algorithm

${\mathbf{c}}_t^Q=W^{DQ}{\mathbf{h}}_t,$

$[{\mathbf{q}}_{t,1}^C,{\mathbf{q}}_{t,2}^C,\dots ,{\mathbf{q}}_{t,n_h}^C]={\mathbf{q}}_t^C=W^{UQ}{\mathbf{c}}_t^Q$

$[{\mathbf{q}}_{t,1}^R,{\mathbf{q}}_{t,2}^R,\dots ,{\mathbf{q}}_{t,n_h}^R]={\mathbf{q}}_t^R=\mathrm{RoPE}(W^{QR}{\mathbf{c}}_t^Q)$

${\mathbf{q}}_{t,i}=[{\mathbf{q}}_{t,i}^C;{\mathbf{q}}_{t,i}^R]$

$\boxed{{\mathbf{c}}_t^{KV}}=W^{DKV}{\mathbf{h}}_t$

$[{\mathbf{k}}_{t,1}^C,{\mathbf{k}}_{t,2}^C,\dots ,{\mathbf{k}}_{t,n_h}^C]={\mathbf{k}}_t^C=W^{UK}{\mathbf{c}}_t^{KV}$

$\boxed{{\mathbf{k}}_t^R}=\mathrm{RoPE}(W^{KR}{\mathbf{h}}_t)$

${\mathbf{k}}_{t,i}=[{\mathbf{k}}_{t,i}^C;{\mathbf{k}}_t^R]$

$[{\mathbf{v}}_{t,1}^C,{\mathbf{v}}_{t,2}^C,\dots ,{\mathbf{v}}_{t,n_h}^C]={\mathbf{v}}_t^C=W^{UV}{\mathbf{c}}_t^{KV}$

${\mathbf{o}}_{t,i}={\sum }_{j=1}^t{\mathrm{Softmax}}_j\left(\frac{{\mathbf{q}}_{t,i}^T{\mathbf{k}}_{j,i}}{\sqrt{d_h+d_h^R}}\right){\mathbf{v}}_{j,i}^C$

${\mathbf{u}}_t=W^O[{\mathbf{o}}_{t,1};{\mathbf{o}}_{t,2};\dots ;{\mathbf{o}}_{t,n_h}]$

where the boxed vectors in blue need to be cached for generation.

Inference optimization

• During inference, the naive formula needs to recover ${\mathbf{k}}_t^C$ and ${\mathbf{v}}_t^C$ from ${\mathbf{c}}_t^{KV}$ for attention.

• Fortunately, due to the associative law of matrix multiplication, we can absorb $W^{UK}$ into $W^{UQ}$, and $W^{UV}$ into $W^O$.

  • Proof below
  • Through this optimization, we avoid the computational overhead for recomputing ${\mathbf{k}}_t^C$ and ${\mathbf{v}}_t^C$ during inference.

• The absorption trick means that head dimension for self-attention is ($r_{kv}+d_r$) during inference, compared to ($d_c+d_r$) during training.

  • Given that for DeepSeek-V2, $r_{kv}$ is set to $4d_c$ and $d_r$ is set to $\frac{d_c}{2}$, then the reduction dimension is about $\frac{\frac{9}{2}}{\frac{3}{2}}=3$ times during inference
  • Thus, we’re trading off KV-cache size for arithmetic intensity

KV cache per token

Attention Mechanism	KV Cache per Token (# Element)	Capability
Multi-Head Attention (MHA)	$2n_h{d}_{c}l$	Strong
Grouped-Query Attention (GQA)	$2n_g{d}_{c}l$	Moderate
Multi-Query Attention (MQA)	$2d_{c}l$	Weak
MLA (Ours)	$(r_{kv}+d_r)l\approx \frac{9}{2}{d}_{h}l$	Stronger

$n_h$ denotes the number of attention heads, $d_c$ denotes the dimension per attention head, $l$ denotes the number of layers, $n_g$ denotes the number of groups in GQA, and $r_{kv}$ and $d_r$ denote the KV compression dimension and the per-head dimension of the decoupled queries and key in MLA, respectively.

The amount of KV cache is measured by the number of elements, regardless of the storage precision. For DeepSeek-V2, $r_{kv}$ is set to $4d_c$ and $d_r$ is set to $\frac{d_c}{2}$. So, its KV cache is equal to GQA with only 2.25 groups, but its performance is stronger than MHA.

Ablations between MQA, GQA, MHA, and MLA

Inference optimizations - Absorption

Multi-Head Latent Attention (MLA) — Inference Absorption Proof

• They key to the proof is to do it on a per-head basis

MLA equations (condensed)

${\mathbf{c}}_t^Q=W^{DQ}{\mathbf{h}}_t,$

${\mathbf{q}}_t^C=W^{UQ}{\mathbf{c}}_t^Q,{\mathbf{q}}_t^R=\mathrm{RoPE}(W^{QR}{\mathbf{c}}_t^Q),{\mathbf{q}}_{t,i}=[{\mathbf{q}}_{t,i}^C;{\mathbf{q}}_{t,i}^R],$

$\boxed{{\mathbf{c}}_t^{KV}}=W^{DKV}{\mathbf{h}}_t,$

${\mathbf{k}}_t^C=W^{UK}{\mathbf{c}}_t^{KV},\boxed{{\mathbf{k}}_t^R}=\mathrm{RoPE}(W^{KR}{\mathbf{h}}_t),{\mathbf{k}}_{t,i}=[{\mathbf{k}}_{t,i}^C;{\mathbf{k}}_t^R],$

${\mathbf{v}}_t^C=W^{UV}{\mathbf{c}}_t^{KV}.$

Per-head scaled scores use $\frac{1}{\sqrt{d_c+d_r}}$: ${\text{score}}_{t,j,i}=({\mathbf{q}}_{t,i}^C{)}^{\top }{\mathbf{k}}_{j,i}^C+({\mathbf{q}}_{t,i}^R{)}^{\top }{\mathbf{k}}_j^R.$

---

Claim A (keys): absorb $W^{UK}$ into the query side

For head $i$, the no-PE part of the dot product is $({\mathbf{q}}_{t,i}^C{)}^{\top }{\mathbf{k}}_{j,i}^C=(W_i^{UQ}{\mathbf{c}}_t^Q{)}^{\top }(W_i^{UK}{\mathbf{c}}_j^{KV})=({\mathbf{c}}_t^Q{)}^{\top }(W_i^{UQ}{)}^{\top }{W}_i^{UK}{\mathbf{c}}_j^{KV}.$

Define the composed matrix and the KV-space query ${\tilde{W}}_i^{QK}\stackrel{\mathrm{def}}{=}(W_i^{UK}{)}^{\top }{W}_i^{UQ}\in {\mathbb{R}}^{r_{kv}\times r_q},{\tilde{\mathbf{q}}}_{t,i}^{KV}={\tilde{W}}_i^{QK}{\mathbf{c}}_t^Q\in {\mathbb{R}}^{r_{kv}}.$

Then $({\mathbf{q}}_{t,i}^C{)}^{\top }{\mathbf{k}}_{j,i}^C=({\tilde{\mathbf{q}}}_{t,i}^{KV}{)}^{\top }{\mathbf{c}}_j^{KV}.$

Consequence. During inference, you only need the cached ${\mathbf{c}}_j^{KV}$ (not ${\mathbf{k}}_{j,i}^C$). Precompute ${\tilde{W}}_i^{QK}$ once and form ${\tilde{\mathbf{q}}}_{t,i}^{KV}$ for the current token. The total score for head $i$ becomes ${\text{score}}_{t,j,i}=\frac{({\tilde{\mathbf{q}}}_{t,i}^{KV}{)}^{\top }{\mathbf{c}}_j^{KV}+({\mathbf{q}}_{t,i}^R{)}^{\top }{\mathbf{k}}_j^R}{\sqrt{d_c+d_r}}.$

(If you prefer a single matrix, stack the blocks: ${\tilde{W}}^{QK}\in {\mathbb{R}}^{(n_h{r}_{kv})\times r_q}$.)

---

Claim B (values): absorb $W^{UV}$ into the output projection $W^O$

Let ${\alpha }_{t,j,i}$ be the attention weights per head. Then ${\mathbf{o}}_{t,i}={\sum }_j{\alpha }_{t,j,i}\underset{{\mathbf{v}}_{j,i}^C}{\underbrace{W_i^{UV}{\mathbf{c}}_j^{KV}}}=W_i^{UV}\underset{{\mathbf{m}}_{t,i}}{\underbrace{\left(\sum _j{\alpha }_{t,j,i}{\mathbf{c}}_j^{KV}\right)}},$ where we defined the compressed-space mixture ${\mathbf{m}}_{t,i}={\sum }_j{\alpha }_{t,j,i}{\mathbf{c}}_j^{KV}\in {\mathbb{R}}^{r_{kv}}.$

Stack ${\mathbf{m}}_{t,i}$ across heads into ${\mathbf{m}}_t\in {\mathbb{R}}^{n_h{r}_{kv}}$ and set $B=\mathrm{blkdiag}(W_1^{UV},\dots ,W_{n_h}^{UV})\in {\mathbb{R}}^{(n_h{d}_c)\times (n_h{r}_{kv})}$. The final output is ${\mathbf{u}}_t=W^O[{\mathbf{o}}_{t,1};\dots ;{\mathbf{o}}_{t,n_h}]=W^{O}B{\mathbf{m}}_t=\underset{{\tilde{W}}^O\in {\mathbb{R}}^{d_{\text{model}}\times (n_h{r}_{kv})}}{\underbrace{\left(W^{O}B\right)}}{\mathbf{m}}_t.$

Consequence. Precompute ${\tilde{W}}^O=W^O\mathrm{blkdiag}(W_1^{UV},\dots ,W_{n_h}^{UV})$. At inference you never materialize ${\mathbf{v}}_{j,i}^C$ or ${\mathbf{o}}_{t,i}$:

1. build ${\mathbf{m}}_{t,i}$ directly in the compressed space from cached ${\mathbf{c}}_j^{KV}$ and weights ${\alpha }_{t,j,i}$,
2. concatenate to ${\mathbf{m}}_t$, and
3. apply ${\tilde{W}}^O$ once to get ${\mathbf{u}}_t$.

---

What to cache (matches the blue boxes)

• $\boxed{{\mathbf{c}}_j^{KV}}\in {\mathbb{R}}^{r_{kv}}$ for each past token $j$ — the low-rank KV cache.
• $\boxed{{\mathbf{k}}_j^R}\in {\mathbb{R}}^{d_r}$ (per head or shared), unchanged by the trick.

No need to cache or recompute ${\mathbf{k}}^C$ or ${\mathbf{v}}^C$.

---

Optimized inference recipe (per new token $t$)

1. Compute ${\mathbf{c}}_t^Q=W^{DQ}{\mathbf{h}}_t$, ${\mathbf{q}}_{t,\cdot }^R=\mathrm{RoPE}(W^{QR}{\mathbf{c}}_t^Q)$, and ${\mathbf{k}}_t^R=\mathrm{RoPE}(W^{KR}{\mathbf{h}}_t)$ (cache ${\mathbf{k}}_t^R$).
2. For each head $i$, compute ${\tilde{\mathbf{q}}}_{t,i}^{KV}={\tilde{W}}_i^{QK}{\mathbf{c}}_t^Q$.
3. Scores: $s_{t,j,i}=(({\tilde{\mathbf{q}}}_{t,i}^{KV}{)}^{\top }{\mathbf{c}}_j^{KV}+({\mathbf{q}}_{t,i}^R{)}^{\top }{\mathbf{k}}_j^R)/\sqrt{d_c+d_r}$.
4. Weights: ${\alpha }_{t,j,i}={\mathrm{softmax}}_j(s_{t,j,i})$.
5. Mix in compressed space: ${\mathbf{m}}_{t,i}={\sum }_j{\alpha }_{t,j,i}{\mathbf{c}}_j^{KV}$.
6. Output: ${\mathbf{u}}_t={\tilde{W}}^O[{\mathbf{m}}_{t,1};\dots ;{\mathbf{m}}_{t,n_h}]$.

All expensive per-token operations after step 1 happen in the low-rank $r_{kv}$ space.

---

Code to absorb $W^{UV}$ into $W^O$

• PR for absorbing w_uk into w_O https://github.com/deepseek-ai/DeepSeek-V3/pull/702
• As before, important to reshape the weights on a per-head basis to absorb correctly

import torch
from torch import nn
 
class AbsorbDemo:
 
    def __init__(self, bsz=1, q_len=1, kv_len=4, dim=7168, kv_lora_rank=512, n_heads=128, v_head_dim=128):
        
        self.n_heads = n_heads
        self.v_head_dim = v_head_dim
        self.dim = dim
        
        self.scores = torch.rand(bsz, q_len, n_heads, kv_len)
        self.kv_cache = torch.rand(bsz, kv_len, kv_lora_rank)
        self.w_uv = torch.rand(n_heads, v_head_dim, kv_lora_rank)
        self.wo = nn.Linear(self.n_heads * self.v_head_dim, self.dim, bias=False) 
        self.wo_absorb = None
        
    def run(self, absorb=False):
        x = torch.einsum("bsht,btc->bshc", self.scores, self.kv_cache)
        if absorb:
            if self.wo_absorb is None:
                wo = self.wo.weight
                wo = wo.transpose(0,1).view(self.n_heads, self.v_head_dim, self.dim)
                self.wo_absorb = torch.einsum("hdc,hdi->hci", self.w_uv, wo)
            x = torch.einsum("bshc,hci->bshi", x, self.wo_absorb)
            x = torch.sum(x, dim=2)
        else:
            x = torch.einsum("bshc,hdc->bshd", x, self.w_uv)   # it cost large memeory
            x = self.wo(x.flatten(2))
        return x
 
 
demo = AbsorbDemo()
tensor1 = demo.run(absorb=False)
tensor2 = demo.run(absorb=True)
print("w/o absorb:", tensor1.data)
print("w   absorb:", tensor2.data)
print(torch.allclose(tensor1.data, tensor2.data, atol=1e-03))
 

MLA Absorption: Why it’s an Inference-Only Optimization

Short answer: It’s great for generation-time reuse (weights frozen; KV cache grows), but awkward or counter-productive for training because of autograd dependencies and compute shape. In the absorbed path the QK reduction per head is $r_{kv}+d_r$, whereas in the canonical training path it’s $d_c+d_r$. The inference win is from never materializing or recomputing ${\mathbf{k}}^C$ and ${\mathbf{v}}^C$ over the growing cache, not from a smaller reduction dimension.

---

Why inference-only (autograd + compute)

1. Autograd dependency.
   The absorbed matrices are products of learnable weights: ${\tilde{W}}_i^{QK}=(W_i^{UK}{)}^{\top }{W}_i^{UQ}$ and ${\tilde{W}}^O=W^O\mathrm{blkdiag}(W_1^{UV},\dots ,W_{n_h}^{UV})$. If you precompute/cache these as constants for speed, then in the graph they don’t depend on $W^{UQ},W^{UK},W^{UV},W^O$, so gradients vanish: $\partial \mathcal{L}/\partial W^{UQ}=\partial \mathcal{L}/\partial W^{UK}=\partial \mathcal{L}/\partial W^{UV}=\partial \mathcal{L}/\partial W^O=0$. That’s fine in eval, but during training it kills learning.

   You could keep ${\tilde{W}}^{QK},{\tilde{W}}^O$ in-graph (no detach) so the chain rule applies: $\partial \mathcal{L}/\partial W^{UK}=(\partial \mathcal{L}/\partial {\tilde{W}}^{QK})W^{U{Q}^{\top }}$ and $\partial \mathcal{L}/\partial W^{UQ}=W^{UK}(\partial \mathcal{L}/\partial {\tilde{W}}^{QK})$ (and similarly for $W^{UV},W^O$). But then you must rebuild these products every forward, keep intermediates for backward, and backprop through extra large matmuls—negating the intended speed/memory win.