Summary
- Block-matrix multiplication is just one layer of abstraction above the usually taught matrix mutliplication
- If we consider the units of computation to be blocks instead of elements, and the operator of the dot product to be matrix-multiply instead of elementwise-multiplication
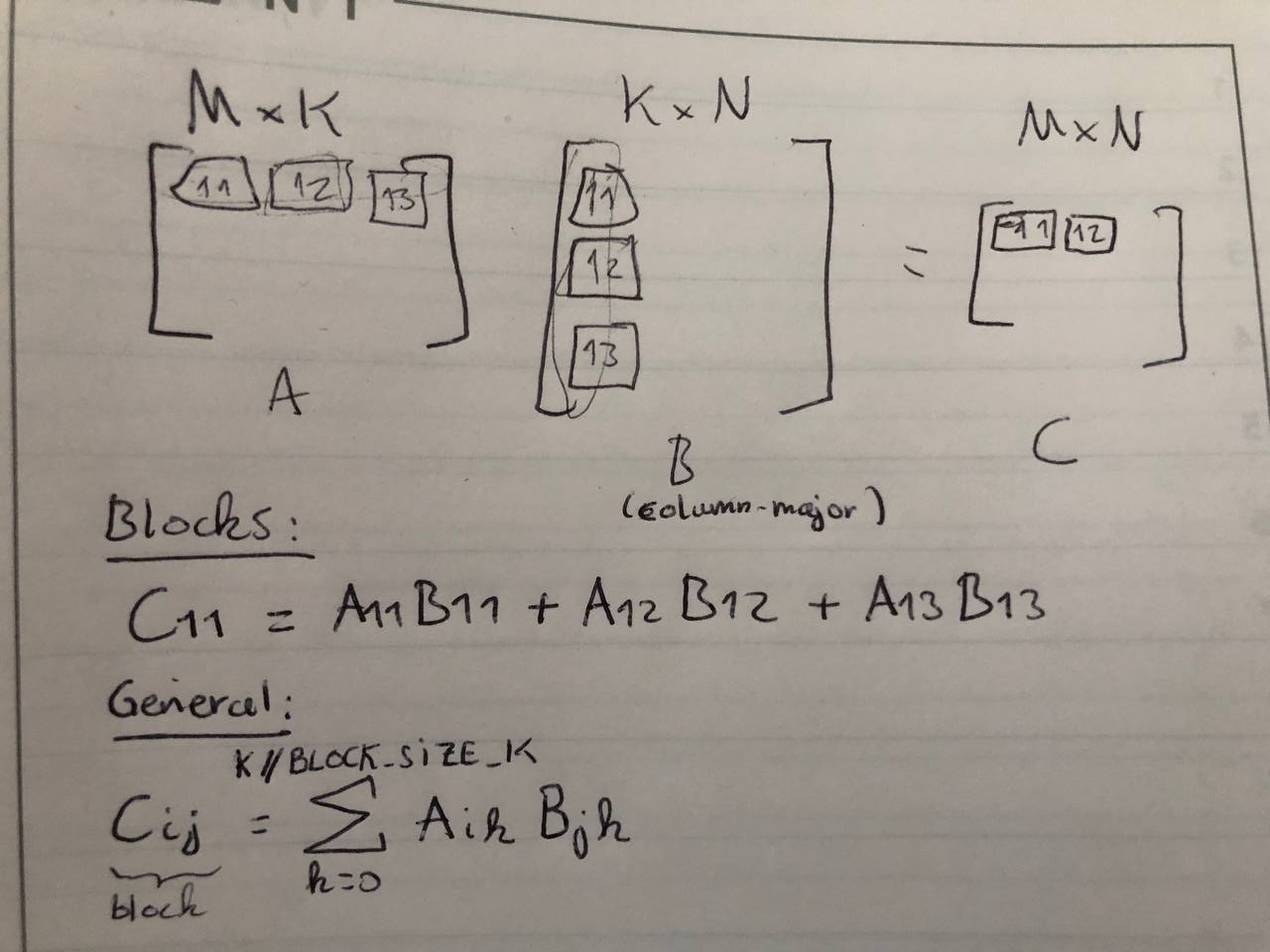
- you can say that is computed by taking the dot product of each row with each column (we accumulate in blocks instead of single output cells)
- you can say that is computed by taking the dot product of each row with each column (we accumulate in blocks instead of single output cells)
Why?
-
Cache blocking and matrix blocking https://www.youtube.com/watch?v=G92BCtfTwOE
- why we use transpose (C= AB, we transpose B such that it becomes “column-major” and reading a column will not result in many cache misses)
-
Cache pollution = data in the cache that we don’t need
-
Cache trashing = continuously fill the cache with data we don’t need
-
If you do matrix mul in the “classical way” i.e. take one row of A and dot-product with every column of B, you’ll end up doing quite a bit of cache trashing/pollution because you read the entire B matrix but it doesn’t fit into cache so it keeps getting evicted
- SOLUTION ⇒ blocking the matrix product
Blocking the matrix product
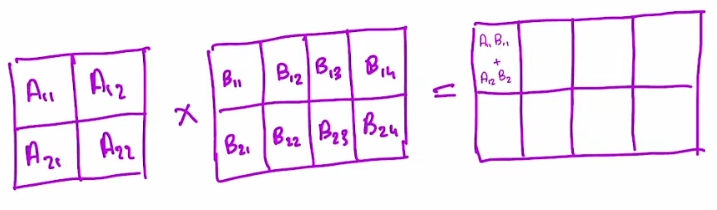
- Break the matmul into blocks
- For the block illustrated below, we need to read the rows 0-3 and columns 0-3. If these rows and columns fit into cache, we will get fewer cache misses
- You can then move on to the next block (keeping rows 0-3 and reading columns 4-7) OR do every block in parallel
- You get a lot of cache misses when you read a new block. but once the rows/columns are cached, the remaining dot products are much faster to compute

Going further and loading only blocks
Non-square blocks
- The inner dimension must match between the two chosen blocksize for A and B
- Thus, a wide and short blocksize (rows < columns) for A implies a tall blocksize for B (usually tall and thin)
- This means few block MMs need to be accumulated for a given output cell ←> one block MMs contributes to few outputs cells
- A tall and thin blocksize (columns > rows) for A implies a short blocksize for B (usually wide and short)
- This implies many block MMs need to be accumulated for a given output cell ←> one block MMs contribute to many outputs cells
- Thus, a wide and short blocksize (rows < columns) for A implies a tall blocksize for B (usually tall and thin)