Summary
- Computing the gradients of a given layer requires both the upper layer gradients and the cached activations .
- This uses a lot of VRAM
- You can decide to drop them and compute them twice (once in forward, again in backward)
- Leads to 20-25% decrease in throughput for a fixed batch size
- Not 50% because forward passes are much more optimized than backward passes
- However, it frees up lots of memory ⇒ can double or quadruple batch size
- Effective throughput may be increased by (100/125)*(2) = 175%
How it works on the low-level
- Reducing Activation Recomputation in Large Transformer Models
- Let be the batch size, sequence length, and hidden size
- The input size to a Transformer block is
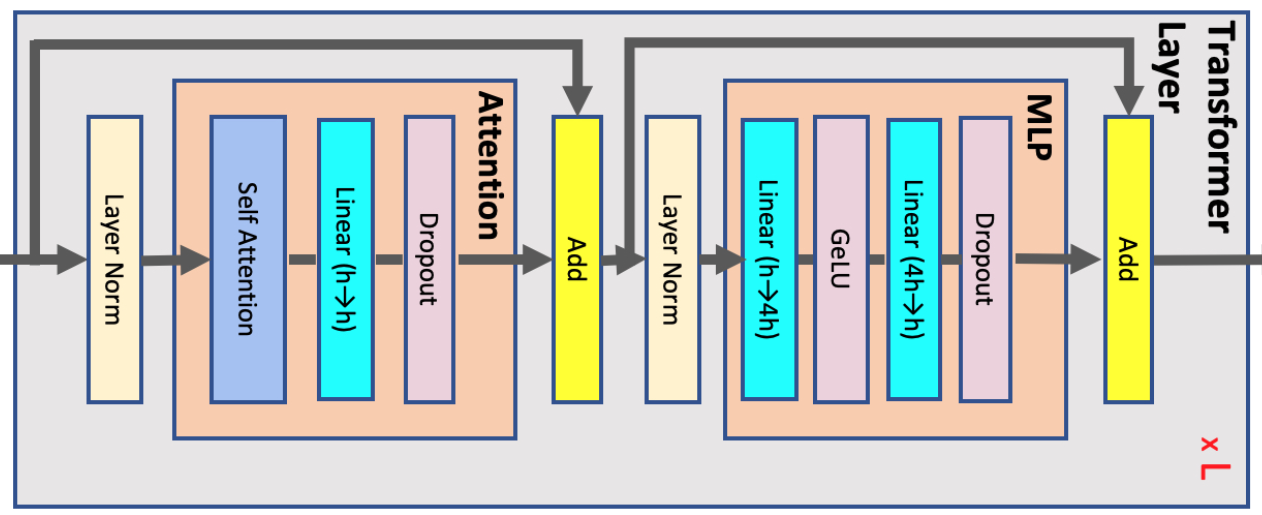
Activation Memory per Transformer Layer
-
Each transformer layer consists of an attention and an MLP block connected with two layer-norms. Below, we derive the memory required to store activations for each of these elements
-
We assume the activation are stored in 16-bit floating format i.e. bytes per element, thus why we multiply often by 2 (compared to by 1 for a boolean mask)
-
We look at what needs to be stored to compute the backward pass
- Remember, as explained in Backpropagation, if , where is the input and a matrix or linear layer,
- ⇒ only need to store the input to the linear layer, to be able to compute the backward pass, since will be provided at the moment of computation
Attention block:
- QKV matrix multiply i.e.
q,k,v = linear_proj(input).split(hidden//3): we only need to store their shared input with size - matrix multiply: It requires storage of both Q and K with total size .
- Softmax: Softmax output with size is required for back-propagation.
- Softmax dropout: Only a mask with size is needed.
- Attention over Values (V): We need to store the dropout output () and the Values () and therefore need of storage.
Summing the above values, in total, the attention block requires bytes of storage.
MLP
- The two linear layers store their inputs with size and . The GeLU non-linearity also needs its input with size for back-propagation. Finally, dropout stores its mask with size . In total, MLP block requires bytes of storage
Layer norm
Each layer norm stores its input with size and therefore in total, we will need of storage.
Total
Full Activation Recomputation
- Now if you only store the transformer layer input and fully recompute the activations, you can get away with only storing 2bsh bytes
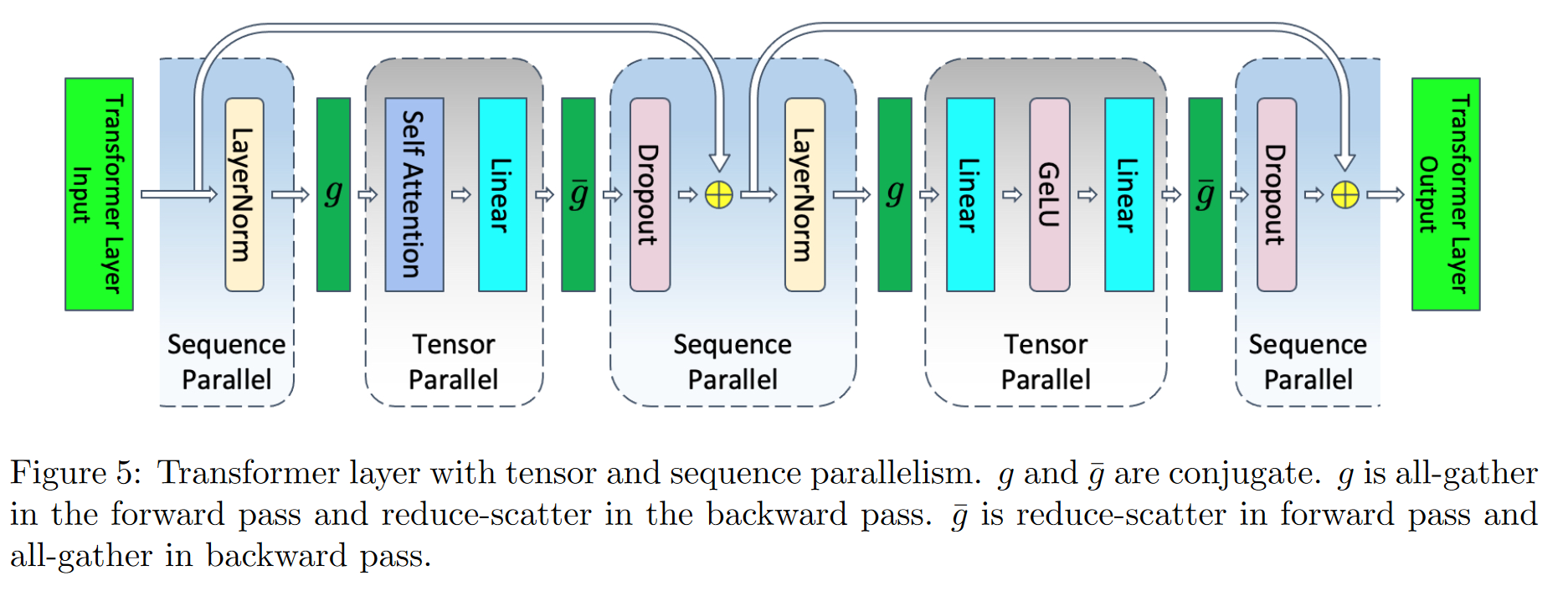
Tensor and Sequence Parallelism as paradigm to reduce activation storage per GPU
Tensor parallelism
- If we parallelize the attention and the MLP blocks
- Not only does tensor parallelism parallelize model parameters and optimizer states inside the attention and MLP blocks, but it also parallelizes the activations inside those blocks.
- Note that the input activations to these blocks (for example input to the Q, K, and V matrix multiplies or input to the h → 4h linear layer) are not parallelized, and only activations within each block are divided across the tensor parallel group
- Assuming -way tensor parallelism, the per-layer memory required to store the activations reduces to (as a single GPU now only cares about the slice of the attention and mlp)
Sequence Parallelism
-
Tensor parallelism, parallelizes the parts of the transformer layer that take the most time during training (attention and MLP) and as a result, it is computationally efficient.
-
However, it leaves the layer-norms as well as the dropouts after attention and MLP blocks intact and as a result, they are replicated across the tensor parallel group.
-
These elements do not require a lot of compute but demand a considerable amount of activation memory
- Quantitatively, the part of the above equation is due to these replicated operations and as a result they are not divided by the tensor parallel size t.
-
The operations are independent along the sequence dimension.
- This characteristic allows us to partition these regions along the sequence dimension s.
- Partitioning along the sequence dimension reduces the memory required for the activations.
- This extra level of parallelism introduces new communication collectives before which will act as converters between sequence and tensor parallel region
- If you’re smart, you can write good communication imperatives and the communication bandwidth used for tensor parallelism and tensor together with sequence parallelism are the same
- Now every operation is well distributed among GPUs, and assuming a sequence parallelism equal to tensor parallelism (which is likely)
Selective recomputation
- The most problematic part (in terms of memory) are the
- Softmax:
- Softmax dropout:
- Attention over Values (V):
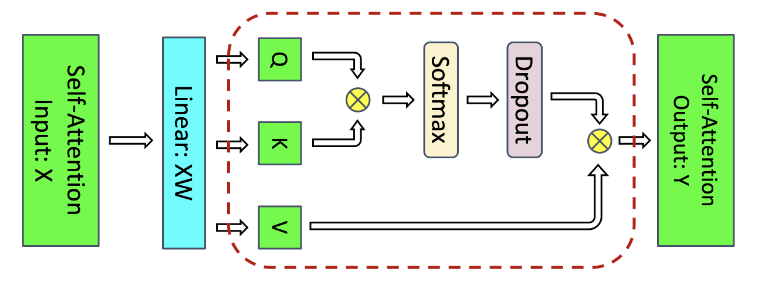
- If we recompute only this part and use tensor + sequence parallelism, we now have
- Using selective activation recomputation allows the required activation memory to scale linearly with sequence length and be independent of the number of attention heads
How to do it in code
In practice
- Just use
from torch.utils.checkpoint import checkpoint
Thorough
- Define a class
CheckpointFunction(torch.autograd.Function)that will need to define aforward()andbackward() - The
forward()will save therun_function,input_tensorsinctx - Do the forward with no gradients i.e.
with torch.no_grad():output_tensors = run_function(*input_tensors)
- At backward time
- add back the
input_tensorsto the computation graphctx.input_tensors = [x.detach().requires_grad_(True) for x in ctx.input_tensors]
- Run the forward with grad_enabled:
with torch.enable_grad():output_tensors = ctx.run_function(*ctx.input_tensors)
- Finally compute the gradients
input_grads = torch.autograd.grad(output_tensors, ctx.input_tensors, output_grads)- return
input_grads
- `torch.autograd.grad(outputs, inputs,grad_outputs=None,…)
- Computes and returns the sum of gradients of outputs with respect to the inputs.
- outputs (sequence of Tensor) – outputs of the differentiated function.
- inputs (sequence of Tensor or GradientEdge) – Inputs w.r.t. which the gradient will be returned (and not accumulated into
.grad). - grad_outputs (sequence of Tensor) – The “vector” in the vector-Jacobian product. Usually gradients w.r.t. each output. None values can be specified for scalar Tensors or ones that don’t require grad.
- add back the