-
ZeRO sits at the Data Parallelism Layer
- super-scalable extension of DP
-
ZeRO removes the memory redundancies across data-parallel processes by partitioning the model states—parameters, gradients, and optimizer state—across data parallel processes instead of replicating them.
Setup
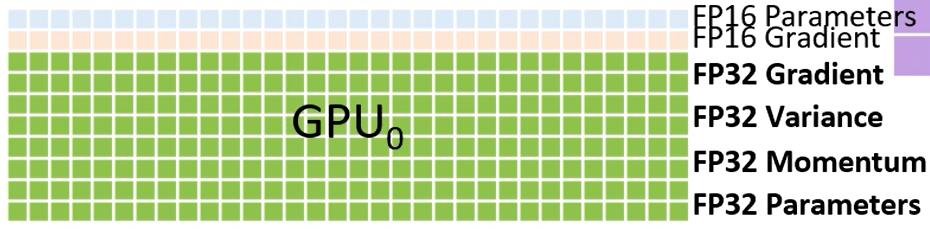
- How memory is organized within a GPU in vanilla DDP
- Let be the number of parameters of the models.
- ”Naive” memory consumption of mixed precision training.
- fp16 copy of the parameters and the gradients, +
- Optimizer states:
- for Adam, as we need to hold fp32 copies of parameters, momentum, and variance
- Total + + =
ZeRO++
- ZeRO++ reduces communication volume by 4x compared to ZeRO-3.
- How?
- Quantized weights (qwZ) : Reduces all-gather parameter communication volume by half by quantizing model weights to int8.
- Hierarchical Partitioning (hpZ): Hierarchical partitioning is a hybrid partitioning scheme that can help in multi-node settings with DeepSpeed ZeRO 3. In this case, you can have model parameter sharding happening within a node, and then have replication across nodes. This means that you don’t have the same amount of memory savings as classic ZeRO-3 running for the full setup, but you avoid expensive inter-node parameter communication overhead, thereby improving throughput in general. Related to hybrid sharding in FSDP (Fully Sharded Data Parallel)
- Quantized gradients (qgZ): Enables even more savings in communication volume by replacing fp16 with int4 quantized data during gradient reduce-scatter ops (Recall: this is the gradient gather + averaging step in ZeRO 2/3 with sharded gradients).
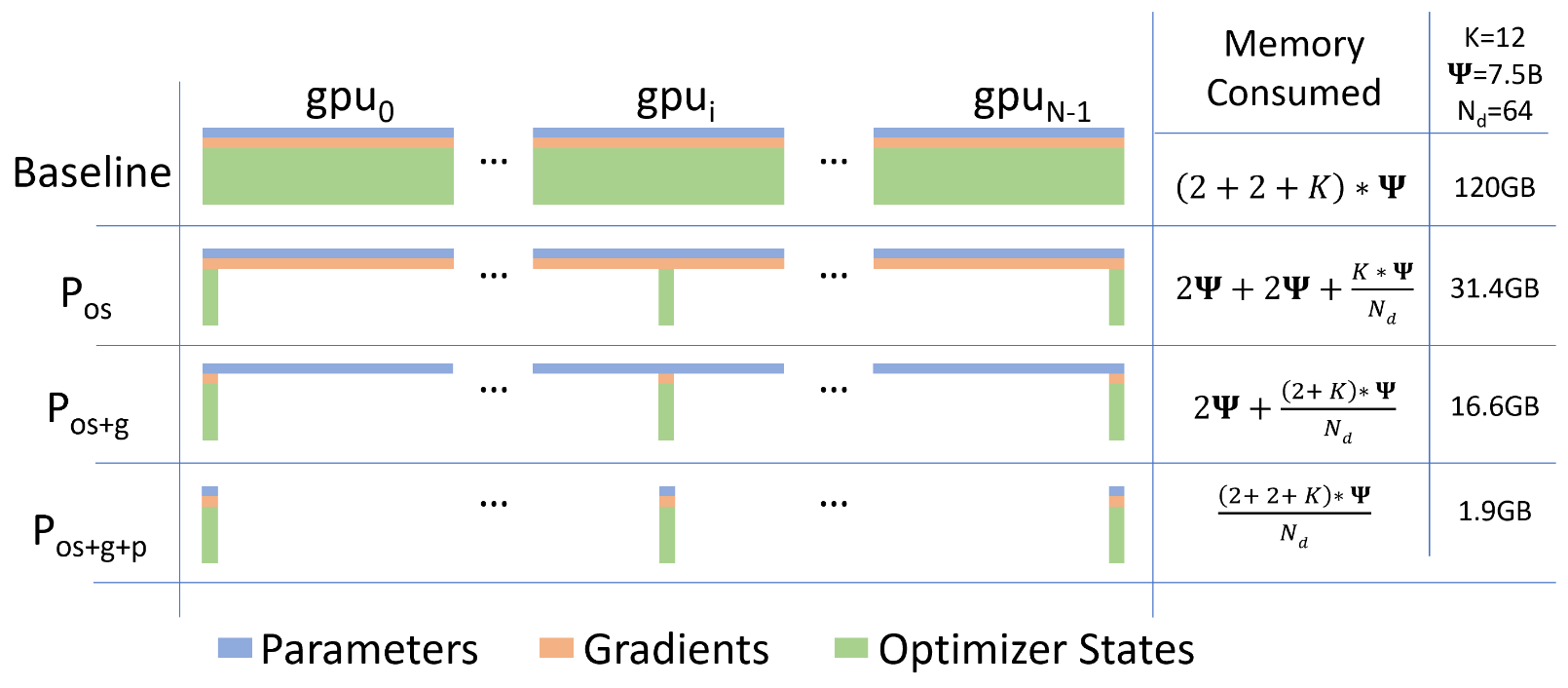
Partitioning (ZeRO-1,2,3)
ZeRO-DP (optimizer state, gradients, parameters)
Let the DP degree be .
: Optimizer State Partitioning
- For a DP degree of , we group the optimizer states into equal partitions, such that the th data parallel process only updates the optimizer states corresponding to the th partition.
- Thus, each data parallel process only needs to store and update of the total optimizer states and then only update of the parameters
- Memory requirements: . If is large, we get approx 4x reduction
: Optimizer State and Gradient Partitioning
- For a DP degree of , we group the optimizer states and the gradients into equal partitions, such that the th data parallel process only updates the optimizer states corresponding to the th partition.
- As each gradient of each layer becomes available during the backward propagation, we only reduce them on the data parallel process responsible for updating the corresponding parameters.
- After the reduction, we no longer need the gradients and their memory can be released on all processes expect the relevant one
- Memory requirements: . If is large, approx. 8x reduction in memory needs.
: Parameter + Optimizer State + Gradient Partitioning
- Just as with the optimizer states, and the gradients, each process only stores the parameters corresponding to its partition.
- When the parameters outside of its partition are required for forward and backward propagation, they are received from the appropriate data parallel process through broadcast.
- The approach only increases the total communication volume of a baseline DP system to 1.5x
- Memory requirements: . If is large, approx. Can fit any model as long as there are sufficient number of devices to share the models states. Reduces consumption by .
Communication volume analysis
- If two communications of volume happen in parallel, we only count a volume of
- What matters is sequential communications, as those will impact performance
All reduce communication volume for gradients in typical DP =
- SOTA implementation of all-reduce use a two step approach: reduce-scatter + all-gather
- reduce-scatter and all-gather both require communication volume. ⇒ communication volume for a single process (but everything overlaps in a ring, so same runtime as doing it with a node)
- sending everything to root node, reducing there, and sending back is also communication volume
- Total volume =
Communication Volume with
- With gradient partitioning, each process only stores the portion of the gradients, that is required to update its corresponding parameter partition.
- During the backward
- Each process sends a gradient of volume to the corresponding partition. Each process does so times over the process of the backward ⇒ volume
- Once the parameters are updated on each process
- Each process sends parameters of volume to all the processes ⇒ volume
- During the backward
- Total volume =
Communication Volume with
-
After parameter partitioning, each data parallel process only stores the parameters that it updates.
-
Therefore, during the forward propagation it needs to receives the parameters for all the other partitions.
-
During the forward
- The responsible process broadcasts its parameters of volume to all other processes, when it’s time to process its layer.
- This happens times.
- Volume =
-
Total volume =