Resources
- Overview of samplers by author of min-p: https://gist.github.com/kalomaze/4473f3f975ff5e5fade06e632498f73e
Basics
- Formally, given a sequence of tokens and a finite vocabulary , where each token , an autoregressive language model models the probability distribution , for each token in the sequence.
How to get the next token
- . (greedy decoding)
- (stochastic sampling)
Temperature sampling
-
Temperature sampling first divides the logits by a temperature parameter before passing them through the softmax function to obtain a modified probability distribution : where is the (unnormalized) log probability of token .
-
The temperature parameter controls the randomness of the sampling process.
- result in a more uniform probability distribution, increasing the chances of sampling lower-probability tokens and generating more diverse output.
- make the distribution sharper, favoring higher-probability tokens and more conservative and deterministic outputs.
Top-p sampling (nucleus sampling)
- Given over the vocabulary at position , top-p sampling first sorts the tokens in descending order of their probabilities.
- It then selects the smallest set of tokens whose cumulative probability exceeds a predefined threshold , where .
- It finally samples according to the re-normalized probabilities.
Sampler Orders
- The order in which samplers are applied matters and can meaningfully change the output.
- For example, if Temperature comes first in the order before top P, then your Temperature value would change the output probabilities that top P judges, and it will truncate differently.
- If top P comes before Temperature, then the original probabilities are measured first, which means Temperature will only affect the tokens you decided to keep using top P.
- It’s usually assumed that temperature sampling is applied first
Beam search
- Beam search is a heuristic search algorithm
- modification of breadth-first seach (BFS) to reduce memory requirements
- How it proceeds
- Start with an initial state (e.g. partly completed generation)
- Generate the next top K candidates (e.g. for tokens, probabilities define the ranking) where K is the beam width
- From each of those K candidates, score all possible states (i.e. tokens)
- Keep only the top K candidates overall
- Start over until a stopping criterion is met (e.g. maximum length or end of text token)
- A beam search with K=1 is equivalent to greedy decoding
- How do you score candidates deeper in the search tree?
- Sum of log probabilities (may tend to favor shorter sequences)
- Average log prob
- Length normalized score
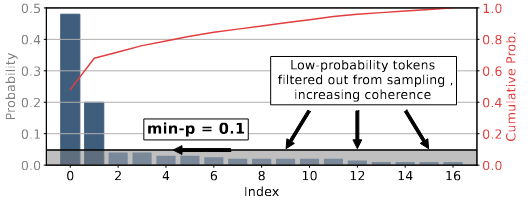
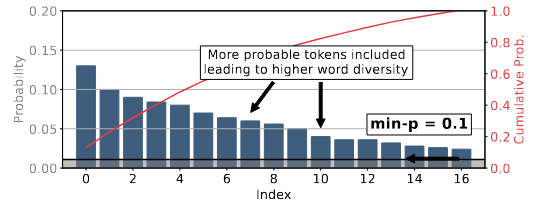
Min-P
Motivation
-
Objectives for min-p are to
- (1) match or outperform the state-of-the-art top-p sampling across various reasoning and performance benchmarks at standard temperature settings between 0 and 1
- (2) better handle the creativity-coherence trade-off at higher temperatures
- (3) provide a simple, effective sampling method without relying on additional techniques like repetition penalties to address the externalities of high-temperature sampling.
-
Top-p sampling does not work well for higher temperatures: here, tokens from the “unreliable tail” can still enter the sampling pool
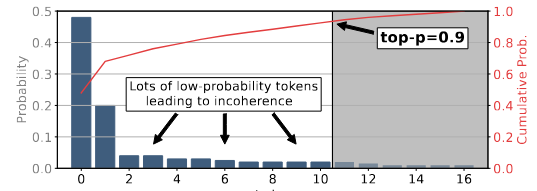
- When using top-p sampling, it is recommended to adjust either the value of p or the temperature τ , but not both simultaneously (OpenAI API, 2024) as they can lead to conflicting effects.
Definition
- The method uses a relative probability threshold to scale the maximum token probability to determine the absolute probability threshold . One can think that
- Sampling is then performed on tokens with probability greater than or equal to .
- Formally, given the maximum probability over the token distribution , the absolute probability threshold is calculated as:
- The sampling pool is then defined as the set of tokens whose probability is greater than or equal to : Finally, the next token is randomly sampled from the set according to the normalized probabilities:
- A lower top-p value results in more selective token choices and a bias towards more likely outputs.
Effects
- High-confidence predictions: When the model assigns high probability to a particular next token, min-p filters out low-probability alternatives. This preserves coherence by avoiding sampling from the “unreliable tail” that could derail generation
- Low-confidence predictions: When there is no clear front-runner, min-p relaxes its filter. This allows the model to sample from a more diverse set of plausible continuations, enabling creativity in open-ended settings.