Summary
Short
-
Larger models are significantly more sample-efficient
- such that optimally compute-efficient training involves training very large models on a relatively modest amount of data and stopping significantly before convergence
-
Performance depends strongly on scale, weakly on model shape
-
Universality of training: Training curves follow predictable power laws, whose parameters are roughly independent of model size
- By extrapolating the early part of the curve, we can predict the loss if trained much longer
Detailed
-
Performance depends strongly on scale, weakly on model shape: Model performance depends most strongly on scale, which consists of three factors: the number of model parameters (excluding embeddings), the size of the dataset , and the amount of compute used for training. Within reasonable limits, performance depends very weakly on other architectural hyperparameters such as depth vs. width
-
Smooth power laws: Performance has a power-law (i.e. logarithmic) with each of the three scale factors , when not bottlenecked by the other two
- low ⇒ capacity too low
- low ⇒ not enough data to generalize
- low ⇒ underfitting
-
Universality of overfitting: Performance improves predictably as long as we scale up and in tandem.
- diminishing returns if or is fixed, while the other increases ⇒ good argument for diff-dataset
- The performance penalty depends predictably on the ratio
- This means, for example, that if we increase model size 8x, we only need to increase the data by roughly 5x to avoid a penalty.
- ⇒ ratio increases by
-
Universality of training: Training curves follow predictable power laws, whose parameters are roughly independent of model size - By extrapolating the early part of the curve, we can predict the loss if trained much longer
-
OOD transfer improves with IID test performance: transfer to a different distribution incurs a roughly constant offset in the loss, but otherwise improves roughly in line with performance on the training set.
-
Sample efficiency: Larger models are more sample-efficient i.e. they reach the same level of performance with fewer optimization steps/tokens processed .
- However this may not be training compute optimal !
- Indeed, given two models and , , e.g. a 1M model and 1B model, let’s say achieves the same loss as in times less samples, it’s still (approximately) times more compute intensive to fit .
- Caveat, the smaller model may never achieve the same loss target we have in mind, so the compute optimality is loss-target dependent
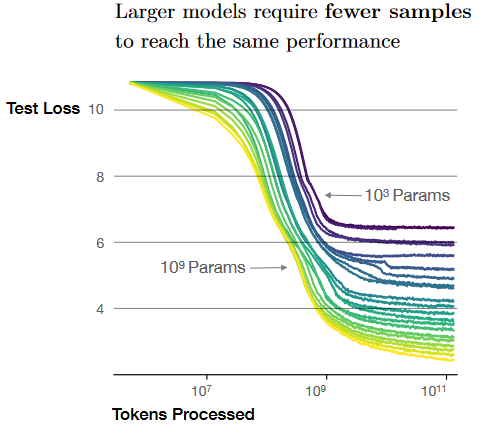
- However this may not be training compute optimal !
-
Training until convergence is not efficient for compute optimality: Given a fixed compute budget , we attain optimal performance by training very large models and stopping significantly short of convergence
- Note that this may not be in contradiction with Chinchilla
- This corroborates with the current “single-epoch” framework, when is very large.
- Data requirements grow very slowly w.r.t training compute i.e.
- 10x the compute , only 2x the data