Linear RNNs and State Space Models (SSMs)

• Hardware-aware architectures

Primer on “Do we need attention?” for sequence modelling

• FFN acts on each position independently

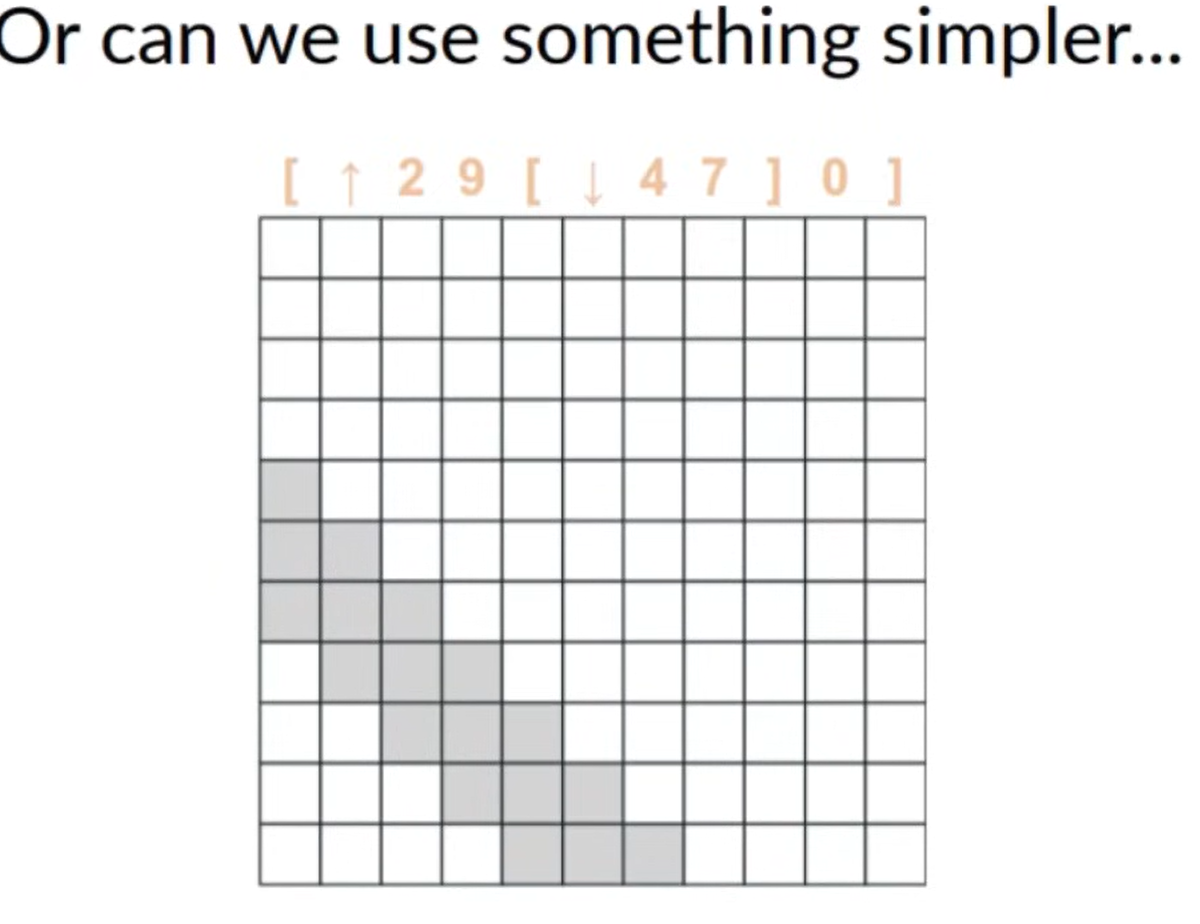
• Attention acts on every position in the sequence.

  • allows us to dynamically look back at all positions when calculating a sequence prediction
  • 

• We could use something simpler

  • 

• Attention is still limited by context length

  • Training Speed - Cost is quadratic in length
  • Generation Speed - Attention requires full lookback

Alternatives to Attention

• Setting: We want to map scalar sequence $u_1,\dots ,u_L$ to scalar sequence $y_1,\dots ,y_L$

How they’re used

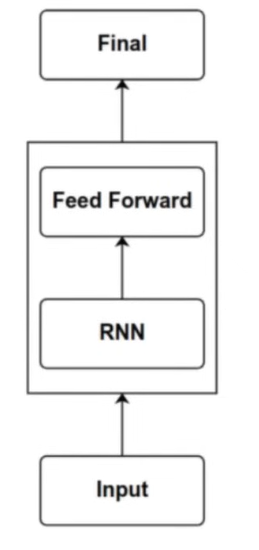
• Similar to a transformer, we just replace the attention in the transformer block by an RNN structure
  • 
• The RNN block takes the input sequence and outputs an output sequence, similarly to a self-attention block
  • The only difference is that the RNN block doesn’t do a full-sequence lookback to compute each value in the sequence, and instead computes a more structured look-back :)

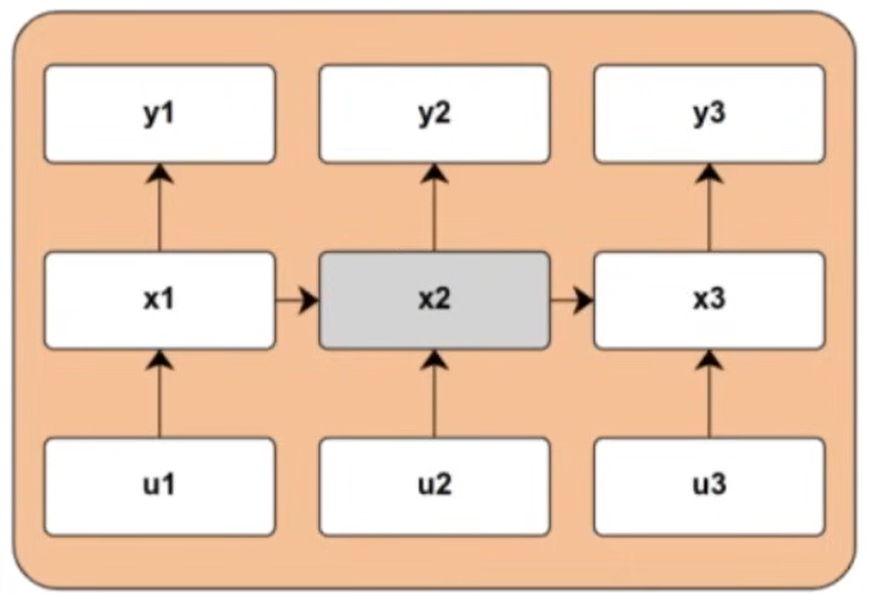
Vanilla RNN

Update rules

• $x_k=\sigma (\bar{A}{x}_{k-1}+\bar{B}{u}_k)$
• $y_k=\bar{C}{x}_k$

Computational graph

• 

Performance

• Training Speed: Slow (Serial bottleneck)
• Generation Speed: Fast (constant-time per step, no need to look back at the entire previous context)

Linear-time variant (LTV) RNNs

Updates rules

• $x_k=({\bar{A}}_k{x}_{k-1}+{\bar{B}}_k{u}_k)$

• $y_k={\bar{C}}_k{x}_k$

• Just construct ${\bar{A}}_k,{\bar{B}}_k,{\bar{C}}_k$ like $Q,K,V$ in Attention, as learnable projections from sequence $x$.

Linear-time invariant (LTI) or Linear RNNs

• Linear RNNS are discretized state space models (SSMs) $\frac{dx(t)}{dt}=Ax(t)+Bu(t)\to x_{k+1}=\bar{A}{h}_k+\bar{B}{u}_k$
• $y(t)=Cx(t)\to y_k=\bar{C}{x}_k$

Updates rules

• $x_k=(\bar{A}{x}_{k-1}+\bar{B}{u}_k)$
• $y_k=\bar{C}{x}_k$

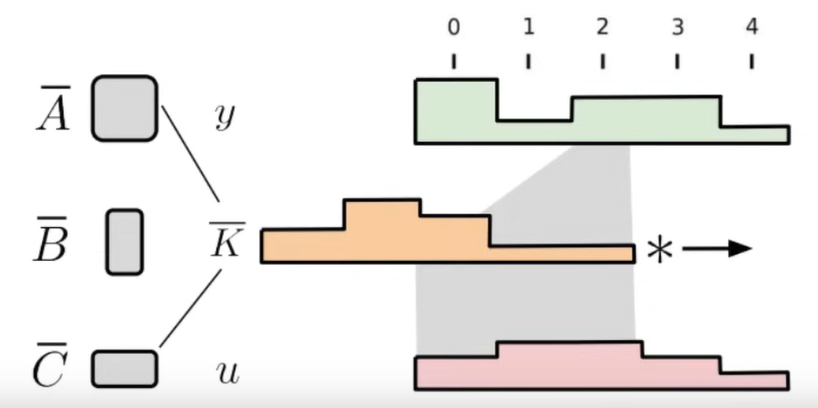
Closed form (rolling out the recurrence)

• $x_{k+1}={\bar{A}}^{k+1}{x}_0+{\sum }_{j=0}^k{\bar{A}}^{k-j}\bar{B}{u}_j$
• Let the kernel $\bar{K}=(\bar{C}\bar{B},\bar{C}\bar{A}\bar{B},\dots \bar{C}{\bar{A}}^{L-1}\bar{B})$ (it’s a vector)
• Then we get a sliding window convolution form $y=conv1d({\bar{K}}_L\dots {\bar{K}}_1,u_1\dots u_L)=\bar{K}\star u$
  • 

Computation 1: Fourier space

• ONLY WORKS FOR LTI SYSTEMS
• You can compute the convolution in Fourier space
  • $y=\bar{K}\star u$
  • map $\bar{K}$ and $u$ into Fourier Space using FFT, $O(LlogL)$
  • compute the product of the individual fourier coefficients $O(L)$
  • map back to time space using iFFT, $O(LlogL)$

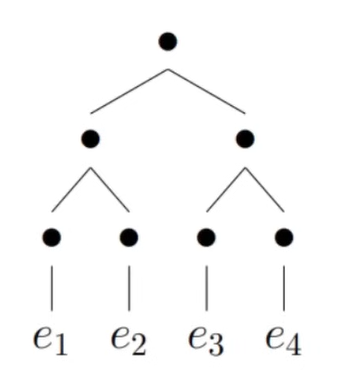
Computation 2: associative scan (S5)

• **It works too for Linear Time Variant RNNs
• (FOR LTI) We have $x_{k+1}={\bar{A}}^{k+1}{x}_0+{\sum }_{j=0}^k{\bar{A}}^{k-j}\bar{B}{u}_j$
• (FOR LTV), it’s not the same but we can write $e_k=({\bar{A}}_k,{\bar{B}}_k{x}_k)$
• We can break up the computation ${\sum }_{j=0}^k{\bar{A}}^{k-j}\bar{B}{u}_j$ into associative terms $e_1\bullet \dots \bullet e_l$ using what’s called a parallel prefix sum algorithm
  • 
• $e_k=({\text{E}}_k,{\text{e}}_k)=(\bar{A},\bar{B}{u}_k)$
• $e_i\bullet e_j=({\text{E}}_i{\text{E}}_j,{\text{E}}_j{\text{e}}_i+{\text{e}}_j)$
• It produces the hidden states $x$ instead of directly outputting $y$
• Based on parallel prefix sum algorithm
  • with a single processor, this algorithm runs in $O(LlogL)$
  • however with around $L$ processors, you can get $O(logL)$

Performance

• Training Speed: Fast (Parallelizable convolution)
• Generation Speed: Fast (constant-time per step, no need to look back at the entire previous context)

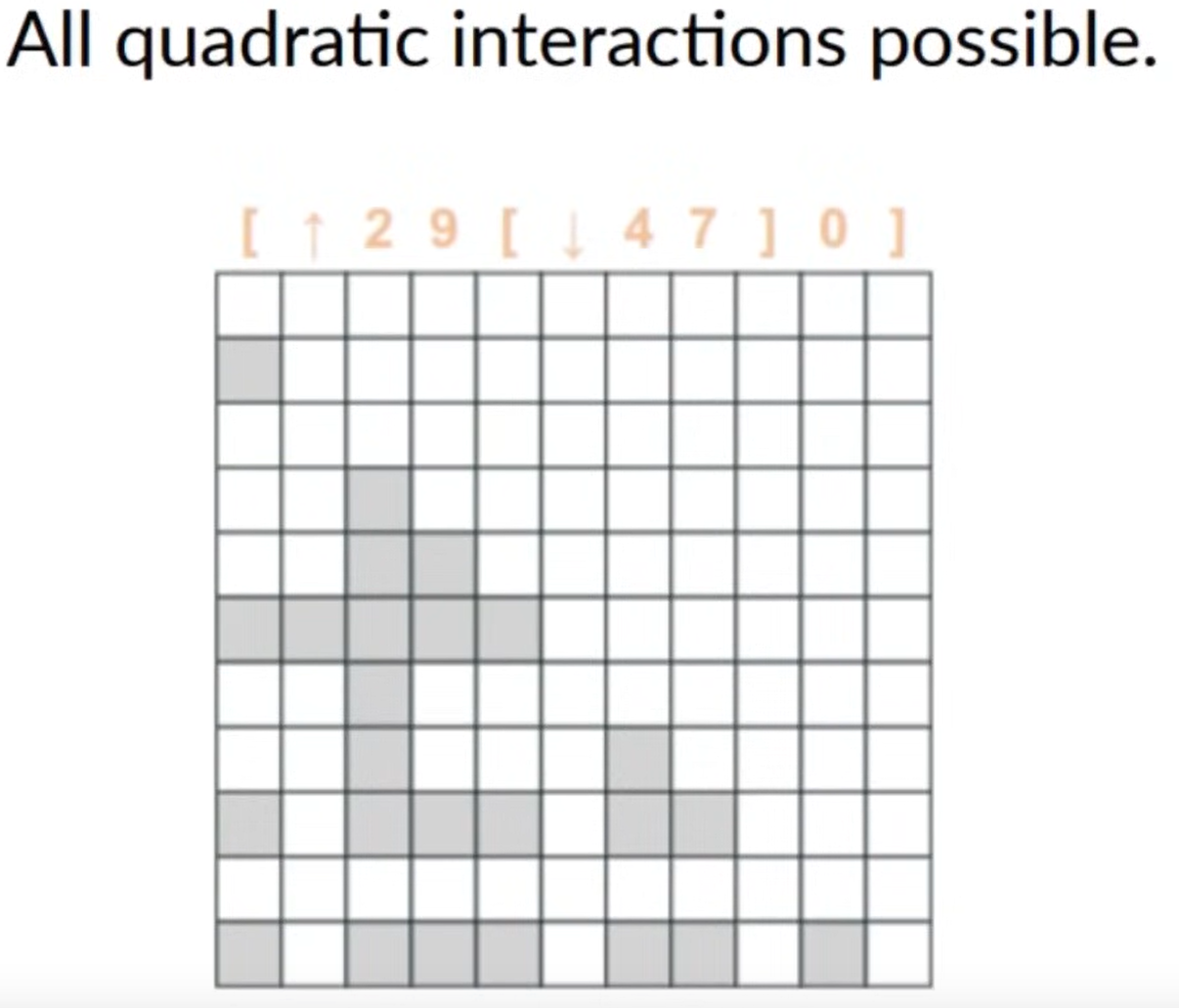
Interactions

• $\bar{A}$ is not dependent on the input (unlike query, keys in the attention)

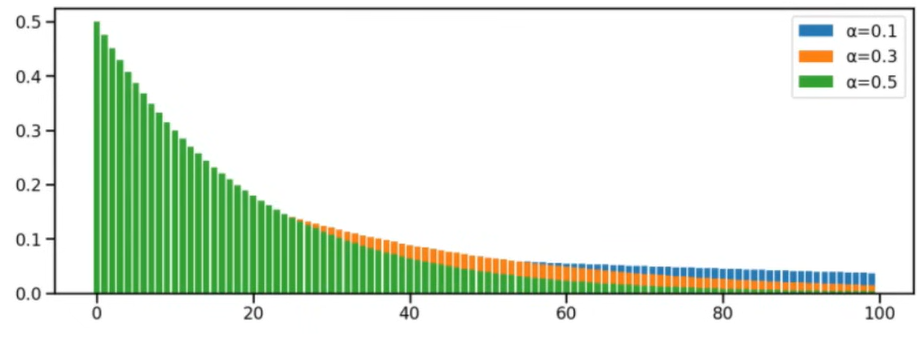
• The choice of the parametrization $\bar{A}$ is critical: stable and informative

  • especially the powers of $\bar{A}$ will influence greatly the kernel $\bar{K}$

• Example

  • LRU paper (periodic):
    • ${\bar{A}}_{j,j}=exp(-exp(v_j)+iexp({\theta }_j))$
    • where $v_j$ and ${\theta }_j$ are learned
    • ${\bar{B}}_j=(1-|{\bar{A}}_{j,j}{|}^2{)}^{1/2}$
  • MEGA (damped, exponential moving average)
    • ${\bar{A}}_{j,j}=1-{\alpha }_j\times {\delta }_j$
    • ${\bar{B}}_j={\alpha }_j$
    • very good results on NLP tasks like translation
    • Kernel visualisation
      • 

• We study the continuous-time differential equation or State Space Model (SSM) to explore the linear RNN parametrization

Kernel Visualization $\bar{K}$

Bidirectional task

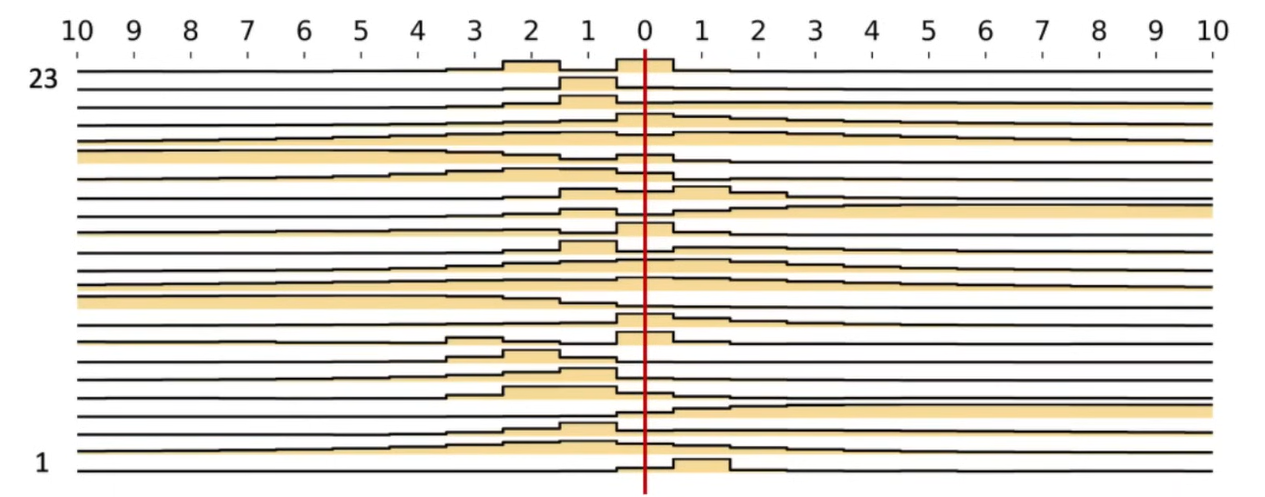
• For a bidirectional or non-causal NLP task (i.e. BeRT)
  • Visualisation from BiGs of a single layer
• Replaces the Attention Matrix
• Single Kernel Per Layer
• All Kernels Visualisation
  • 

Performance issues

• Linear RNNs really shine in very long context, but don’t have huge savings yet in smaller context

Issues on Accelerators

• Support for complex numbers
• Support for FFT (lower precision, TPU)
• Numerical Stability
• Fast Associative Scans
• Hard to compete with pure MatMul in Attention

RWKV

•