Abstract
- You need to think about matrix shapes both in terms of:
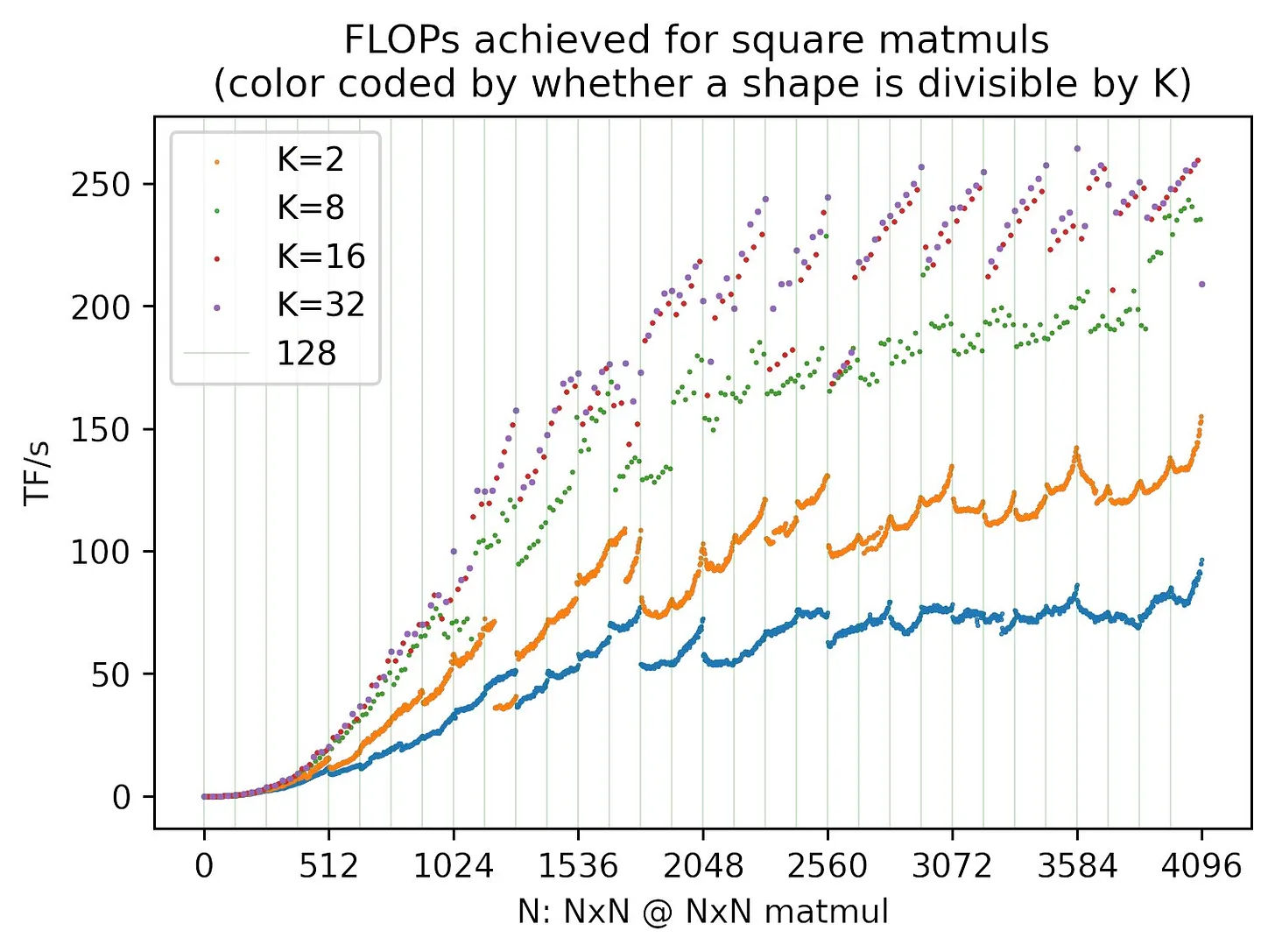
- Is it a nice power of 32 e.g. divisible by 32 ?
- so that it fits nicely both in cache/shared memory
- so that it fits nicely into tiles (e.g. a matrix 257x128) requires two tiles instead of 1
- is the total number of tiles just below or equal the number of SMs (or divisible by)
- e.g. A100 has 108 SMs and a matrix tile (256x128) grid has dimensions and . That gives us tiles.
- Is it a nice power of 32 e.g. divisible by 32 ?
- While it’s super important that sequence length and hidden size and various other hyper parameters are high multiples of 2 (64, 128 and higher) to achieve the highest performance, because in most models the batch dimension is flattened with the sequence length dimension during the compute, the micro batch size alignment usually has little to no impact on performance
What Shapes Do Matrix Multiplications Like?
Memory Layout of Tiling
-
Let’s think about how our matrix’s memory layout looks like when our size is a multiple of the cache line (pretend it’s 128 bytes or 4 fp32 numbers). We’ll show 3-4 cache lines
-
Each matrix row starts on a cache line ! If we need the second row, we can just load the 3 cache lines that the yellow elements are a part of
-
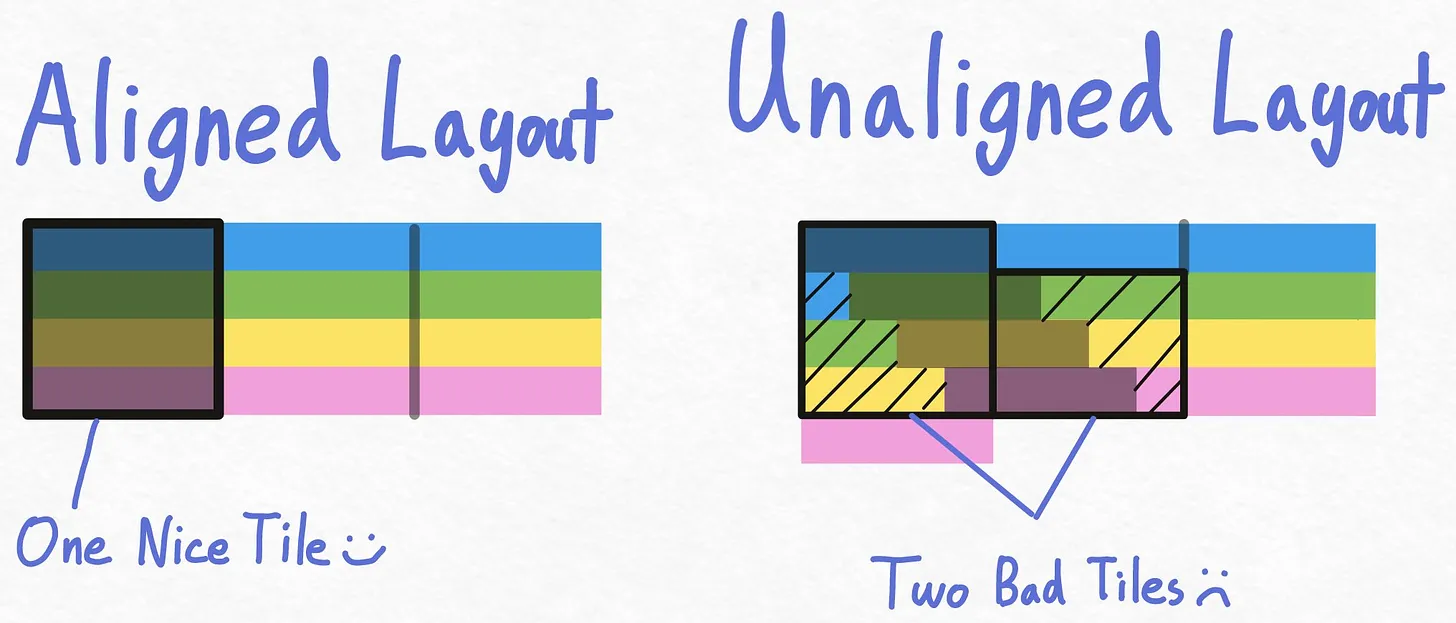
What happens if we increase the number of elements per row from 12 to 13
-
With the unaligned layout, things are much messier. For example, in order to load the first 4 green elements, we must issue 2 loads! One that gets the last blue element + the first 3 green elements, and one that gets the 4th
GPU matrix mul implementation
- GPUS implement matrix mul by partitioning the output matrix into tiles, which are then assigned to thread blocks.
- Tile size, in this guide, usually refers to the dimensions of these tiles. Each thread block computes its output tile by stepping through the K dimension in tiles, loading the required values from the A and B matrices, and multiplying and accumulating them into the output.
- where the dimensions are
Quantization
Main idea
Let’s say we have N parallel tasks (which each take a second) and N CPUs.
Q: How long does it perform to take all tasks?
A: 1 second
Q: What about if we have (N+1) parallel tasks, and N CPUs?
A: 2 seconds(!) Now, one CPU must perform two tasks, taking a total of 2 seconds.
Wave quantization
- Wave quantization is the example above, except with CPUs ⇒ SMs and tasks ⇒ thread blocks.
- More details as to what these are in GPU architecture.
- Here the total number of tiles is quantized to the number of multiprocessors on the GPU
Applied example
-
An NVIDIA A100 GPU has 108 SMs; in the particular case of 256x128 thread block tiles, it can execute one thread block per SM, leading to a wave size of 108 tiles that can execute simultaneously. Thus, GPU utilization will be highest when the number of tiles is an integer multiple of 108 or just below.
- For square multiplication where are
- If , our tile grid has dimensions and . That gives us 98 tiles. Since an A100 has 108 SMs, that’s still one wave
- If , we get tiles, or 2 waves!
-
As your matrix size increases, the total number of tiles/blocks increases. When this crosses a multiple of the # of SMs, your perf drops since you need to execute an additional “wave”.