Scaling Laws - rules we expect to hold
- Scaling Laws for Batch Size
- The optimal batch size is proportional to the gradient noise scale (the sum of the variances of the individual gradient components, divided by the global norm of the gradient). This tends to be large for noisy RL environments, and smaller for well defined tasks.
- Scaling Laws for Neural Language Models
- Larger models are significantly more sample-efficient
- such that optimally compute-efficient training involves training very large models on a relatively modest amount of data and stopping significantly before convergence
- Performance depends strongly on scale, weakly on model shape
- Universality of training: Training curves follow predictable power laws, whose parameters are roughly independent of model size
- By extrapolating the early part of the curve, we can predict the loss if trained much longer
- Larger models are significantly more sample-efficient
More parameters
- Why: better performance
- Problems: instabilities (loss spikes, tuning)
- Solution:
- qk-layernorm, z-loss (Tricks to reduce instabilities)
- keeps attention logits and outputs logits from diverging
- mu-Transfer, which gives us
- feature learning stability ( i.e. “typical element size” of vectors and is with respect to width .)
- hyperparameter stability, which ensures that the optimal HPs for small models remain unchanged as the model size grows.
- qk-layernorm, z-loss (Tricks to reduce instabilities)
More FLOPs
- Why: more throughput
- for a fixed model size, increasing your number of effective FLOPs directly translates to more token processed per second ⇒ better model fixed amount of GPU hours
Solution: FP8
-
theoretical increase in FLOPs from bf16: 2x
-
Problems: numerical instability
-
Solution:
- per-tensor scaling FP8-LM Training FP8 Large Language Models
- u-mup, enforcing a variance of 1 for both activation and gradients (ensures that floating-point representations during training stay within the range of a given number format.)
Solution: Kernels
- Writing kernels allows for more optimized GPU utilization, which usually focuses on reducing the amount of memory transfers, as this is the main bottleneck for GPU computation
- leverage hardware-specific characteristics (e.g. Hopper TMA)
- fusing multiple operations together to limit memory transfers (e.g. adding residuals, scaling)
Less FLOPs for same capacity
- Why: Similar to above, for a fixed model capacity, reducing the required FLOPs directly translates to more tokens processed per second
Solution: Adaptive computation
- ”Adaptive width”
- Mixture of Experts (MoE)
- reduces required number of FLOPs in the feed-forward needed to be spent to process a given token
- validated at scale
- ”Adaptive depth”
- Mixture of Depth paper (tokens may skip some layers)
- not validated at scale (if DeepMind published it, it’s probably because it doesn’t work at scale, at least in its current form)
- “Adaptive modality”
- MoMa: Efficient Early-Fusion Pre-training with Mixture of Modality-Aware Experts
- specific modality token goes to its specific experts
- The insight driving our approach is the inherent heterogeneity of modalities: text and image have distinct information and redundancy patterns
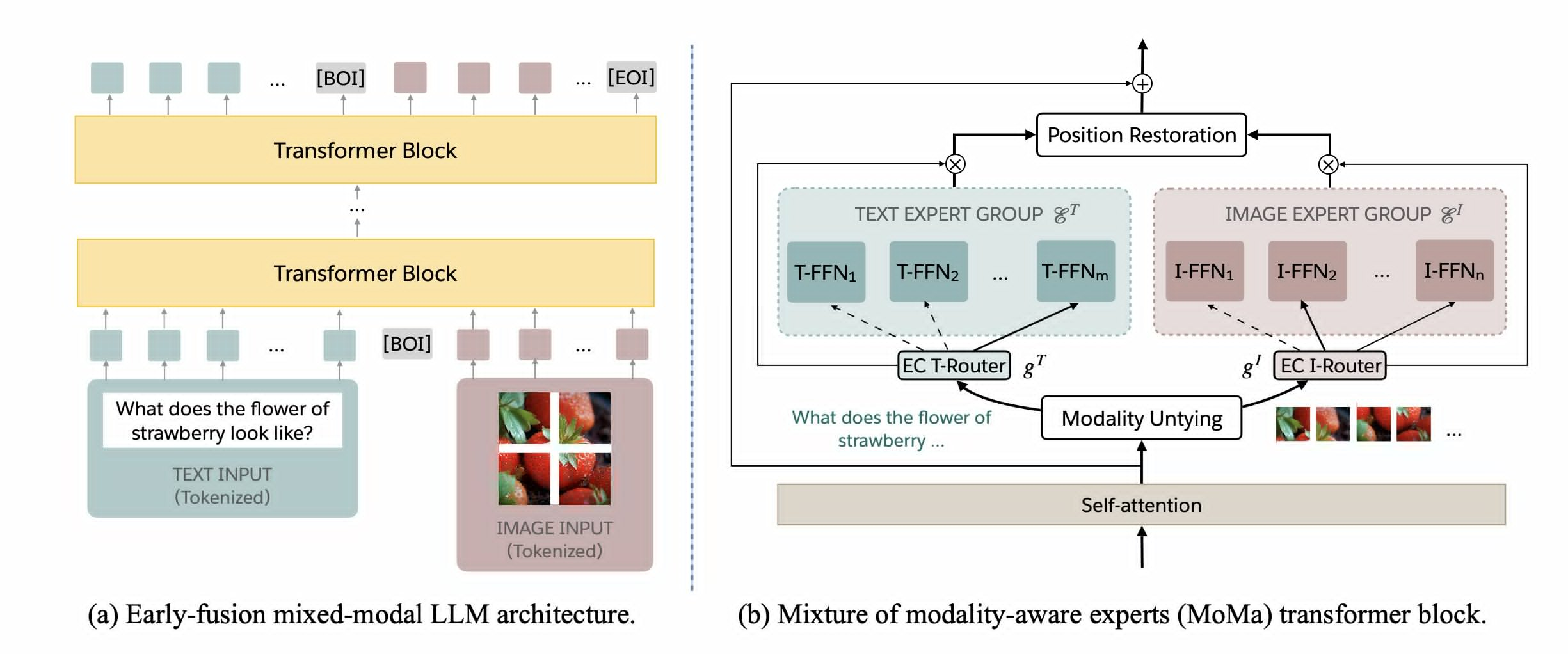
- MoMa: Efficient Early-Fusion Pre-training with Mixture of Modality-Aware Experts