Summary
- ALL THE CONCLUSIONS ONLY HOLD IN THE LOW DATA REGIME, WHEN THERE’S NOT ENOUGH FINETUNING DATA
- When data is limiting performance
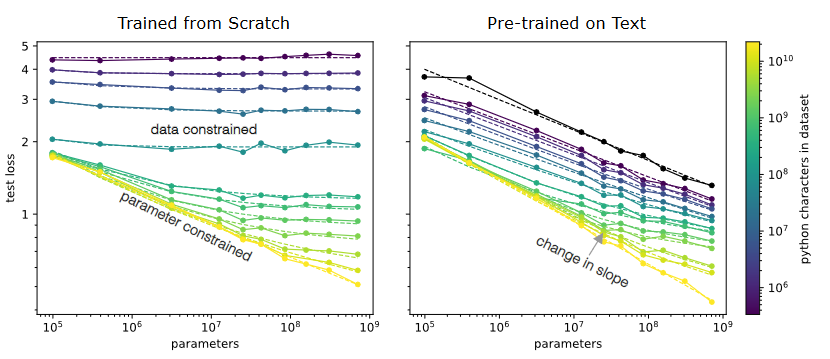
- Classic/OLD supervised ML: When we train increasingly large neural networks from-scratch on a fixed-size dataset, they eventually become data-limited and stop improving in performance (cross-entropy loss)
- Unsupervised, fine-tuning setting. When we do the same for models pre-trained on a large language dataset, the slope in performance gains is merely reduced rather than going to zero
- Takeaways
- In the low data regime, the effective amount of data transferred by pre-training can be around 100x the size of the finetuning data.
- Given an estimation for your particular problem.
- One can make choices w.r.t to collecting more data v.s. increasing model size.
- Indeed, for example, for transfer from text to python we have .
- So increasing the data-set size by a factor, , would be worth approximately the same as increasing the model size, , by .
- In other words, a 10x increase in model size, , would be worth approximately a 100x increase in fine-tuning dataset size, , under these conditions.
- One can make choices w.r.t to collecting more data v.s. increasing model size.
- How to estimate
- Fine-tune a model with a 1% and 10% of the existing dataset.
- Vary the model size given the full fine-tuning dataset and estimate the lost performance in terms of a reduction in model size.
- Check Appendix B and C for how to fit the power laws
Detailed
Units of data
- The paper focuses on units of data, while holding everything else fixed.
- They calculate the effective data “transferred” from pre-training by determining how much data a transformer of the same size would have required to achieve the same loss when training from scratch.
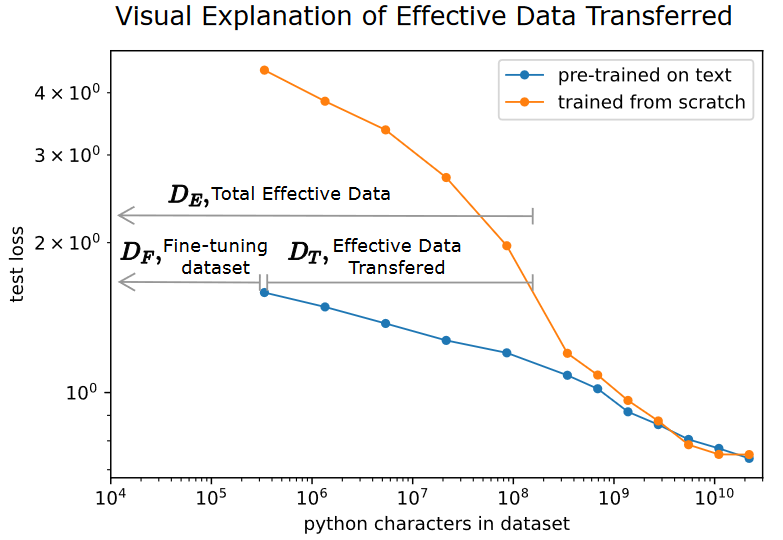
- is the amount of additional python characters that a from-scratch model of the same size would have needed to achieve the same loss on python as a fine-tuned model.
- In the labeled example, we see that for a 40M parameter transformer, fine-tuned on 3e5 characters, is approximately 1000x bigger than .
- The less fine-tuning data is available, the more pre-training helps.
- In the limit, they are the same, as the model will learn the distribution perfectly
Power Laws
-
Target: generating python code
-
They find that the effective data transferred is described well in the low data regime by a power-law of parameter count and fine-tuning dataset size.
- (pretrained on text and other programming languages)
- (pretrained on text only)
- The larger value indicates that mixture of distributions transfer more readily than plain text in the low-data regime, while the smaller means the benefit diminishes as we approach the high-data regime.
-
When comparing pre-training on text and pre-training on an equal mix of text and non-python code, they found identical scaling with model size, the exponent .
- Thus the exponent beta appears to depend only on the model architecture and target distribution.
- they hypothesize that it measures how the model architecture generalizes on the target distribution.
-
The quantity provides a useful measure of the directed proximity of two distributions, with smaller indicating closer proximity.
- Measurements of are cheap and enable one to make principled trade-offs between collecting expensive fine-tuning data and increasing model size.
- For transfer from text to python we have so increasing the data-set size by a factor, , would be worth approximately the same as increasing the model size, , by In other words, a 10x increase in model size, , would be worth approximately a 100x increase in fine-tuning dataset size, , under these conditions.
Data Multiplier
- An implication of the power law is that pre-training effectively multiplies the fine-tuning dataset, , in the low-data regime. We find the multiplier formulation helpful in building intuition. Note that the multiplier goes down as increases.
- If is fixed, increasing by 10x effectively multiplies the data by
- In the limit of very extensive pretraining, may approach 1, and increasing directly increases the effective data by the same amount.
- When data is limiting performance i.e. fixed and small, the pre-trained models have a better scaling law i.e. they are able to quickly improve even on small amounts of data