-
“Understanding Diffusion Models: A Unified Perspective” + “Variational Diffusion” from Kingma
-
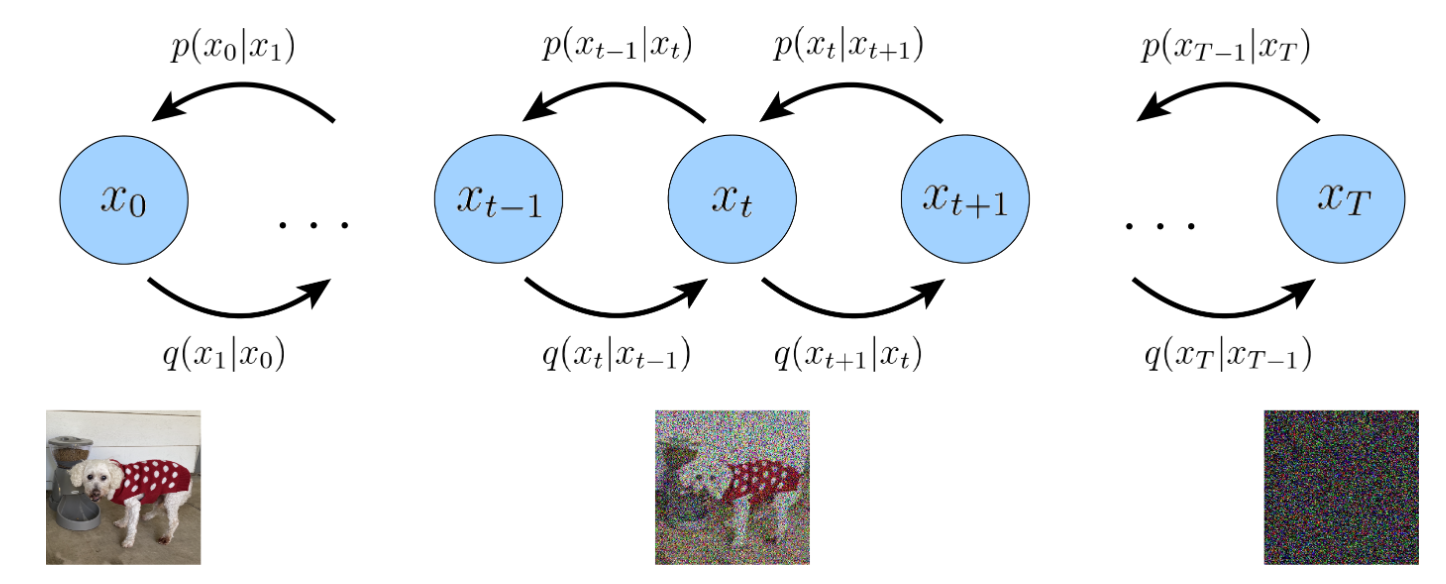
The easiest way to think of a Variational Diffusion Model (VDM) is simply as a Markovian Hierarchical Variational Autoencoder with three key restrictions:
- The latent dimension is exactly equal to the data dimension
- This means that . Everything stays in space.
- The structure of the latent encoder at each timestep is not learned
- It is pre-defined as a linear Gaussian model. In other words, it is a Gaussian distribution centered around the output of the previous timestep
- The Gaussian parameters of the latent encoders vary over time in such a way that the distribution of the latent at final timestep is a standard Gaussian
- The latent dimension is exactly equal to the data dimension
-
Diagram
ELBO derivation
The variational lower bound loss is derived from where we take advantage of the fact that both and are Markovian, and thus the log-product can be easily decomposed into incremental steps.
- We obtain
- Reconstruction term
- where the first term is the reconstruction term, like its analogue in the ELBO of vanilla VAE.
- This term can be approximated and optimized using a Monte Carlo estimate
- where the first term is the reconstruction term, like its analogue in the ELBO of vanilla VAE.
- Denoising matching terms
- the terms are denoising matching terms.
- We learn desired denoising transition step as an approximation to tractable, ground truth denoising transition step (which closed form is derived in The diffusion process)
- Detail: when originally deriving the ELBO, you get “consistency terms”
- i.e. , where a denoising step from a noisier image should match the corresponding noising step from a cleaner image.
- However, actually optimizing the ELBO using the terms we just derived might be suboptimal; because the consistency term is computed as an expectation over two random variables for every timestep, the variance of its Monte Carlo estimate could potentially be higher than a term that is estimated using only one random variable per timestep.
- The trick to obtain denoising matching terms is to rewrite the encoder transition as , where the extra conditioning is superfluous due to the Markov property and then use Bayes rule to rewrite each transition as
- the terms are denoising matching terms.
- Prior matching term
- The last form enforces isotropic Gaussian at the end of the diffusion, it’s never optimized.
Optimizing in practice
Maximizing ELBO, equivalent to denoising (when variance schedule is fixed)
-
Remember that using Bayes theorem, one can calculate the posterior in terms of and which are defined as follows:
- (posterior variance schedule)
-
The KL-divergence between two Gaussian disitributions is composed of an MSE of the two means (divided by some variance term) + some terms about the variances
-
In the case, where we fix the variance schedule ,
- we can match exactly the two distributions variances, and thus minimizing the KL-divergence is exactly equivalent to minimize the MSE between the two means ⇒ denoising objective:
- By setting (similar parametrization as ), we recover:
- Optimizing a VDM boils down to learning a neural network to predict the original ground truth image from an arbitrarily noisified version of it
- Just do
Learning Diffusion Noise Parameters (variance schedule is not fixed)
- Above, we wrote our per-timestep objective as
- By plugging in in the above equation, we get
- Recall that .
- Then following the definition of the signal-to-noise ratio (SNR) as , we can write
- . In a diffusion model, we require the SNR to monotonically decrease as timestep increases.
Parametrizing the SNR
- We can directly parameterize the SNR at each timestep using a neural network, and learn it jointly along with the diffusion model.
- As the SNR must monotonically decrease over time, we can represent it as:
- where is modeled as a monotonically increasing neural network with parameters .
- We can write elegant forms for the ‘s
Optimizing everything
- We now optimize
- where we showed above that