-
https://lilianweng.github.io/posts/2023-01-10-inference-optimization/#sparsity
-
Sparsity is an effective way to scale up model capacity while keeping model inference computationally efficient. We consider two types of sparsity_
- Sparsified dense layers, including both self-attention and FFN layers.
- Sparse model architecture; i.e. via incorporating the Mixture-of-Experts (MoE) component.
N:M Sparsity via Pruning
-
N:M sparsity is a structured sparsity pattern that works well with modern GPU hardware optimization, in which out of every consecutive elements are zeros.
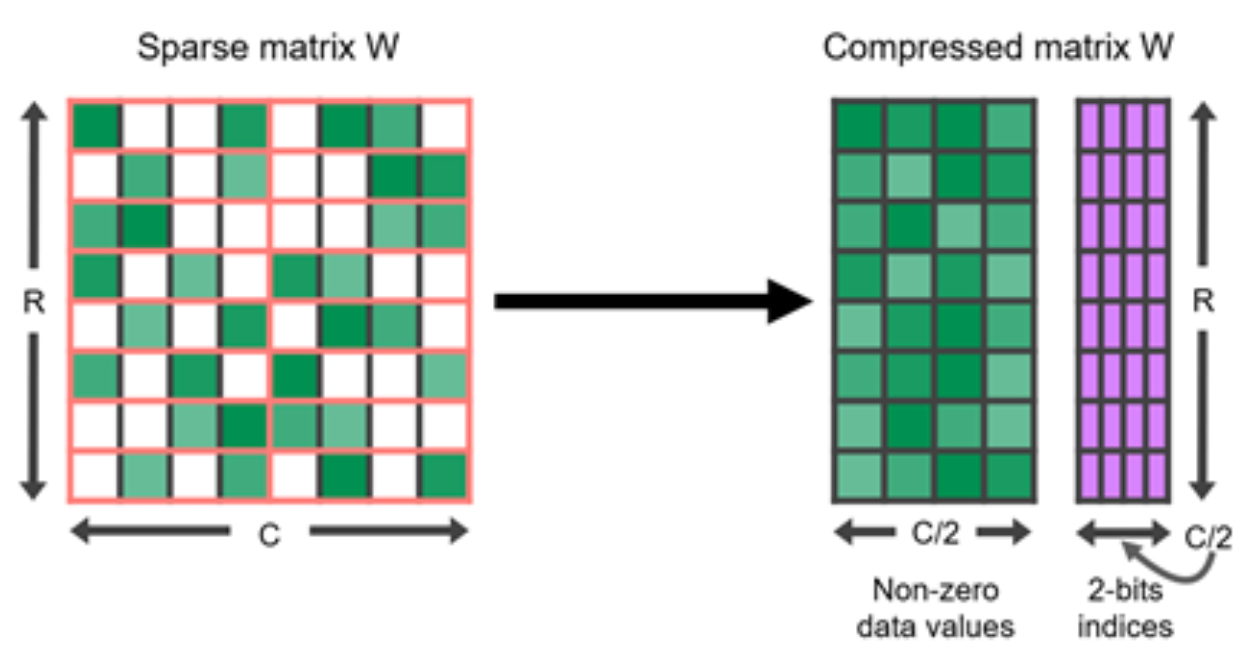
- For example, the sparse tensor core of Nvidia A100 GPU has support for 2:4 sparsity for faster inference
- Relevant, Kernel for fast 2:4 sparsification (50% of zeros),
- Example of 2:4 matrix and its compressed representation
-
To sparsify a dense neural network to follow a N:M structured sparsity pattern, Nvidia (2020) suggested using the three-step routine workflow for training a pruned network: train –> prune to satisfy 2:4 sparsity –> retrain.
Iterative greedy permutation algorithm
-
Permuting columns can provide more options in the pruning process to maintain parameters of large magnitude or to satisfy a special restriction like N:M sparsity (Pool & Yu 2021).
- As long as paired axes of two matrices are permuted in the same order, the results of matrix multiplication would not change.
-
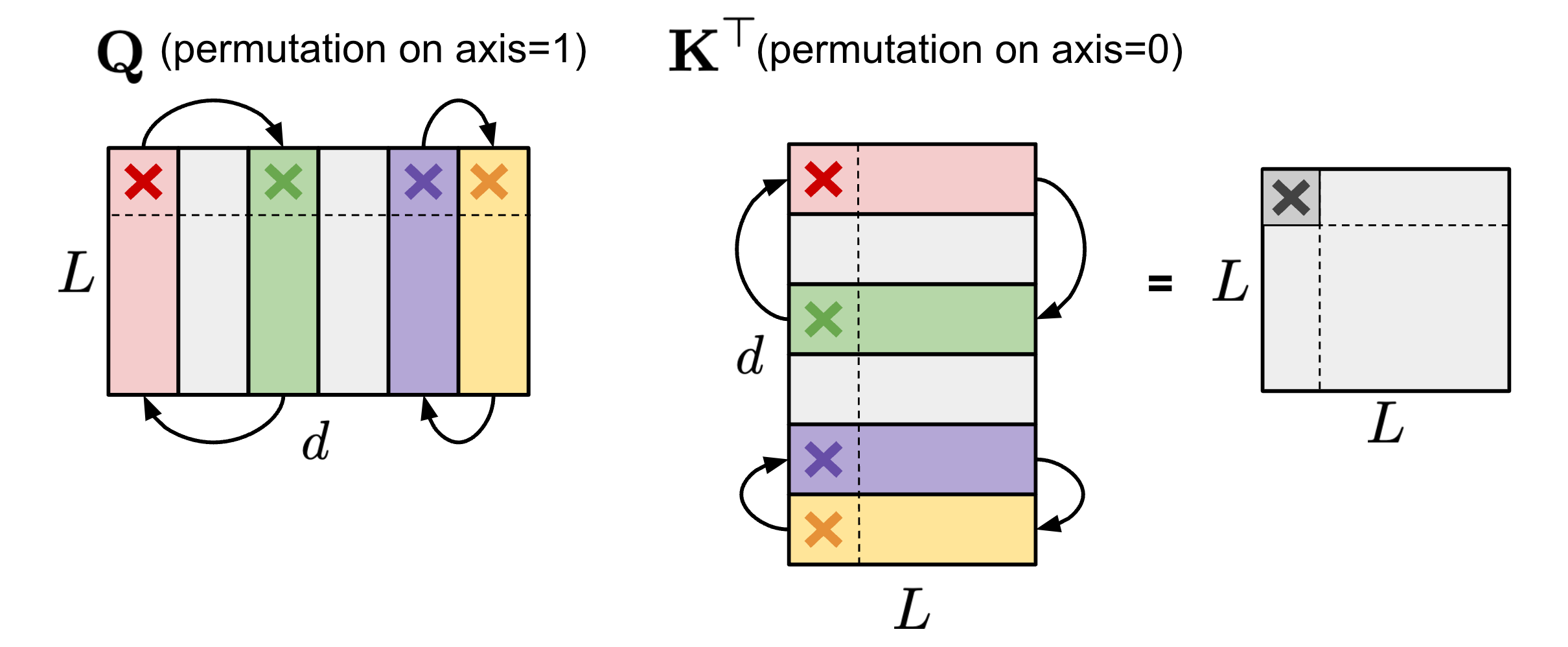
Self-attention permutation
- Within the self-attention module, if the same permutation order is applied on the axis 1 of query embedding matrix and the axis 0 of key embedding matrix , the final result of matrix multiplication of would stay the same.
- Within the self-attention module, if the same permutation order is applied on the axis 1 of query embedding matrix and the axis 0 of key embedding matrix , the final result of matrix multiplication of would stay the same.
-
FFN permutation
- The same applies. Within the FFN layer that contains two MLP layers and one ReLU non-linear layer, we can permute the first linear weight matrix along the axis 1 and the second linear weight matrix along the axis 0 in the same order.
-
To enforce N:M structured sparsity, let’s split the columns of one matrix into multiple slides of columns (named “stripe”)
- We can easily observe that both the order of columns within each stripe and the order of stripes have no effect on the N:M sparsity restriction. (because the N:M restriction is local to each stripe)
-
Pool & Yu (2021) proposed an iterative greedy algorithm to find optimal permutation that maximizes the weight magnitude for N:M sparsity.
- The network can achieve better performance if it was permuted before pruning, compared to pruning the network in its default channel order
- All pairs of channels are speculatively swapped and only the swap that leads to the greatest increase in magnitude is adopted, generating a new permutation and concluding a single iteration.
- Greedy algorithm may only find local minima, so they introduced two techniques to escape local minima:
- Bounded regressions: In practice two random channels are swapped, up to a fixed number of times. The solution search is limited to a depth of only one channel swap to keep the search space broad and shallow.
- Narrow, deep search: Choose multiple stripes and optimize them at the same time.
Training a model with N:M sparsity from scratch
SR-STE
-
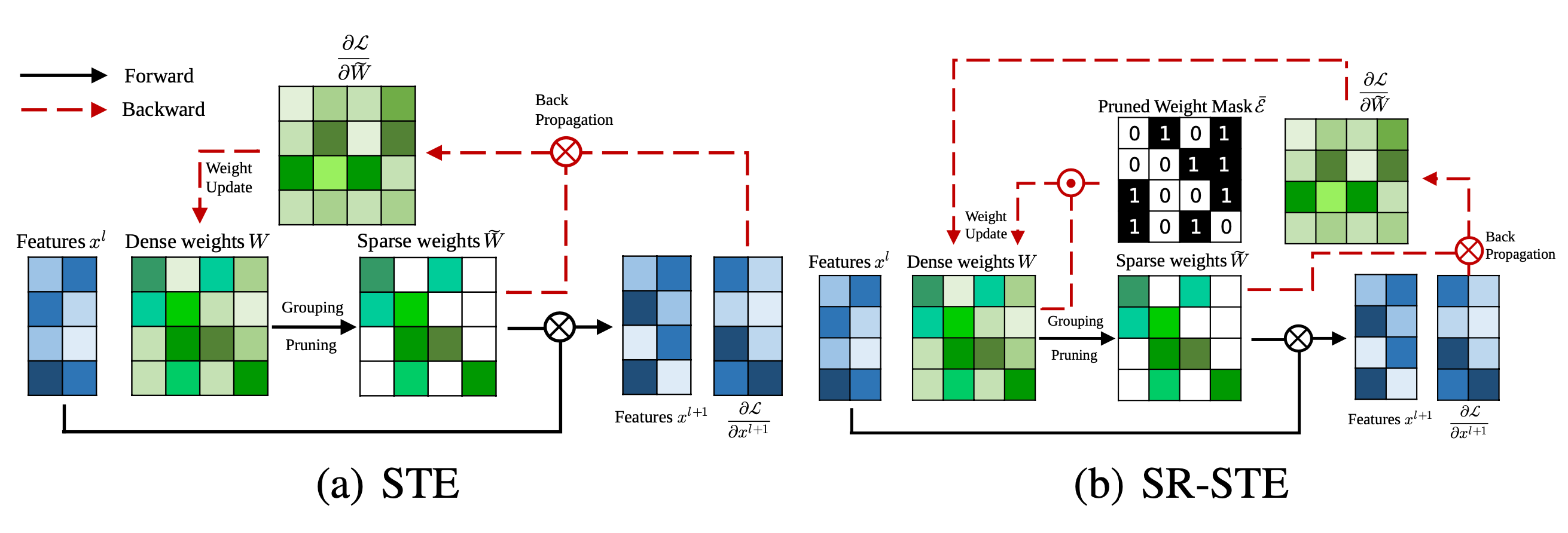
To train a model with N:M sparsity from scratch, SR-STE extended STE (Straight-Through Estimator; Bengio et al. 2013), which is commonly used for back-propagation update in model quantization, to work for magnitude pruning and sparse parameter update.
-
Original STE computes the gradients of dense parameters wrt the pruned network , , and applies that to the dense network as an approximation:
-
The extended version, SR-STE (Sparse-refined STE), updates the dense weights by:
- where is the mask matrix for and is element-wise multiplication
- SR-STE is proposed to prevent large change in the binary mask by (1) restricting the values of weights pruned in and (2) promoting the non-pruned weights in
-
Comparison between STE and SR-STE
Top-KAST
- Different from STE or SR-STE, the Top-KAST (Jayakumar et al. 2021) method can preserve constant sparsity throughout training in both the forward and backward-passes but does not require forward passes with dense parameters or dense gradients.