- https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-quantization
- https://github.com/ggerganov/llama.cpp/pull/1684
- https://github.com/ggerganov/llama.cpp/discussions/5063
Definitions
- k-quants is a hierarchical quantization scheme. It works on blocks.
Blocks
- The weights of a given layer are split into “super” blocks each containing a set of “sub” blocks.
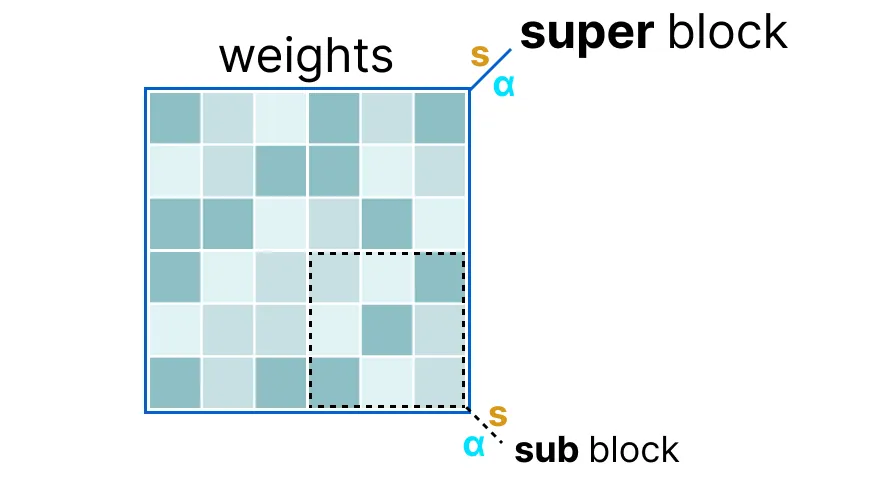
- Each sub-block computes its (maximum value) and scale factor AND also quantizes its underlying values.
- Then the super-block takes the scale factors of each sub-block, and quantizes them, which requires the super-block to have a scale factor itself.
How the scale is found in llama.cpp
- llama.cpp has a general implementation to find the scale of a given row of values that minimizes quantization error and can take importance weights for each value (can be important for sensitive layers e.g. how this weight can be found is discussed in Second order information for quantization (how to find outliers))
- General implementation of llama.cpp goes through the code to find the optimal scaling for type-0 quantization
Quantization types
-
In the existing
ggmlquantization types we have- ”type-0” (
Q4_0,Q5_0)- weights
ware obtained from quantsqusingw = d * q, wheredis the block scale. - (absmax-quantization)
- weights
- “type-1” (
Q4_1,Q5_1) In “type-1”,- weights are given by
w = d * q + m, wheremis the block minimum. - (asymmetric quantization)
- weights are given by
- ”type-0” (
-
In depth example:
GGML_TYPE_Q2_K- “type-1” 2-bit quantization in super-blocks containing 16 blocks, each block having 16 weight. Block scales and mins are quantized with 4 bits. This ends up effectively using2.5625bits per weight (bpw)- Computing bits per weights:
- 2 bit per weight
- for the scale and min of a single block
- for the scale of the super-block (always in fp16)
- which adds up to
2.5625bits per weight
- Computing bits per weights: