Chain-of-Thought (CoT) Paradigm

Why CoT

• CoT, introduced by Wei et al. (2023), enables an LLM to condition its generation on its intermediate reasoning steps when answering multi-step problems, thereby augmenting the LLM’s reasoning ability on complex problems such as math word problems.
• This technique is really useful for improving performance on complicated reasoning tasks that would require humans to spend more than one second solving. Tokens can have very different information density, so give language models time to think.

How to elicit CoT

• few-shot or zero-shot prompting
• instruction tuning on substantial amount of chain-of-thought (CoT) reasoning data
• CoT-decoding Chain-of-Thought Reasoning without Prompting

Chain-of-Thought Reasoning without Prompting

https://arxiv.org/pdf/2402.10200

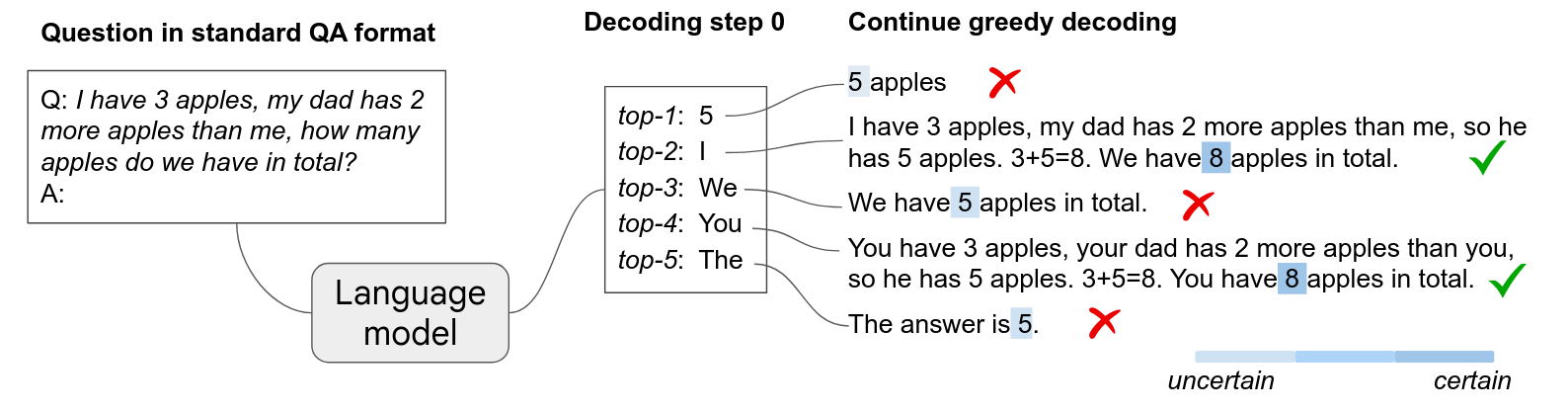
• CoT reasoning paths can be elicited from pre-trained LLMs by simply altering the decoding process. Rather than conventional greedy decoding, they investigate the top-𝑘 alternative tokens, uncovering that CoT paths are frequently in these sequences.

• The presence of a CoT in the decoding path correlates with a higher confidence in the model’s decoded answer

  • This confidence metric effectively differentiates between CoT and non-CoT paths.
  • 

• The method can be combined with a zero-shot CoT prompt

Chain-of-Thought (CoT) Decoding

• Models employing greedy decoding often does not contain a CoT path

  • opting to solve problems directly. This tendency may stem from the model’s skewed perception of problem difficulty, shaped by its pre-training on predominantly simpler questions.

• LLMs can reason if we consider the alternative decoding paths.

  • exploring alternative top-𝑘 (𝑘 > 0) tokens at the first decoding step.

Extracting CoT Paths (answer confidence)

• They found that the presence of a CoT path typically leads to a more confident decoding of the final answer, characterized by a significant probability disparity between the top and secondary tokens: ${\Delta }_{k,\text{answer}}=\frac{1}{|\text{answer}|}{\sum }_{x_t\in \text{answer}}p(x_t^1|x_{<t})-p(x_t^2|x_{<t}).$

• Here $x_t^1$ and $x_t^2$ represent the top two tokens at the $t$-th decoding step in the $k$-th decoding path, chosen for their maximum post-softmax probabilities from the vocabulary, given $x_t$ being part of the answer tokens (e.g. for a GSM8K, it might be all tokens that represent a number).

  • The model’s overall confidence in decoding the final answer is approximated by averaging these probability differences for all relevant answer tokens $x_t$. For example, for a GSM8K question, given the answer “60”, they average the probability differences for all tokens in that answer, i.e., “6” and “0”.

• Computing the answer confidence $\Delta$ requires identifying the answer spans

  • One common approach used for public models is to extract the last numerical value in math reasoning tasks
  • or the final option in set-based reasoning tasks, as the answer, following the Tülu evaluation
  • Alternatively, you can extend the model’s output with the prompt “So the answer is”, and then align these continuations with spans in the model’s decoding path as the answer.

Aggregation of the decoding paths

• The method decodes the top-k paths
  • There’s no guarantee that the majority answer is likely to be the correct one (which is assumed by self-consistency), if the model has a tendency to easily fall into erroneous paths.
• The method proposes weighted aggregation method, i.e., they take the answer that maximizes: ${\tilde{\Delta }}_a={\sum }_k{\Delta }_{k,a}$ where ${\Delta }_{k,a}$ is the $k$-th decoding path whose answer $=a$.
  • It stabilizes the result.