TLDR
- Are pretrained much faster vs. dense models
- Have faster inference compared to a model with the same number of parameters
- Require high VRAM as all experts are loaded in memory
- Face many challenges in fine-tuning, but recent work with MoE instruction-tuning is promising
Definition
In the context of transformer models, a MoE consists of two main elements:
- Sparse MoE layers are used instead of dense feed-forward network (FFN) layers
- A gate network or router, that determines which tokens are sent to which expert.
- In practice, gating is just weighted multiplication
- If G is close to zero, we don’t compute the expert
- Usually,
Cons
- Training: MoEs enable significantly more compute-efficient pretraining, but they’ve historically struggled to generalize during fine-tuning, leading to overfitting.
- Inference: fast but high VRAM usage
- Effective batch size reduced: uneven batch sizes, underutilization for certain experts, could have “dead” experts
Routing
Load balancing tokens for MoEs
- An auxiliary loss is added to encourage giving all experts equal importance. This loss ensures that all experts receive a roughly equal number of training examples.
- Router z-loss, introduced in ST-MoE, significantly improves training stability without quality degradation by penalizing large logits entering the gating network. Since this loss encourages absolute magnitude of values to be smaller, roundoff errors are reduced, which can be quite impactful for exponential functions such as the gating
- Random routing: in a top-2 setup, we always pick the top expert, but the second expert is picked with probability proportional to its weight.
Expert capacity
- maximum number of tokens routed to a given expert. If an expert is at capacity, the token is considered overflowed, and it’s sent to the next layer via residual connections (or dropped entirely in other projects).
- Switch transformers use
- Switch Transformers perform well at low capacity factors (1-1.25)
Noisy Top-K Gating
- We add some noise (for load balancing)
- We pick the top i.e. set to if not in top
- Softmax
Fine-tuning MoEs
-
The overfitting dynamics are very different between dense and sparse models. Sparse models are more prone to overfitting.
- We can explore higher regularization (e.g. dropout) within the experts themselves (e.g. we can have one dropout rate for the dense layers and another, higher, dropout for the sparse layers)
-
Only updating the MoE layers leads to a huge performance drop
-
Only freezing the MoE layers speeds up and reduce memory for fine-tuning + works well
-
Sparse models tend to benefit more from smaller batch sizes and higher learning rates
-
A recent paper, MoEs Meets Instruction Tuning (July 2023), performs experiments doing:
- Single task fine-tuning
- Multi-task instruction-tuning
- Multi-task instruction-tuning followed by single-task fine-tuning
-
Multi-task instruction-tuning followed by single-task fine-tuning works really well
Making MoEs go brrr
- Initial MoE work presented MoE layers as a branching setup, leading to slow computation as GPUs are not designed for it and leading to network bandwidth becoming a bottleneck as the devices need to send info to others.
Parallelism
- Expert parallelism: experts are placed on different workers. If combined with data parallelism, each core has a different expert and the data is partitioned across all core
Capacity Factor and communication costs
- Increasing the capacity factor (CF) increases the quality but increases communication costs and memory of activations. If all-to-all communications are slow, using a smaller capacity factor is better. A good starting point is using top-2 routing with 1.25 capacity factor and having one expert per core. During evaluation, the capacity factor can be changed to reduce compute
Efficient training
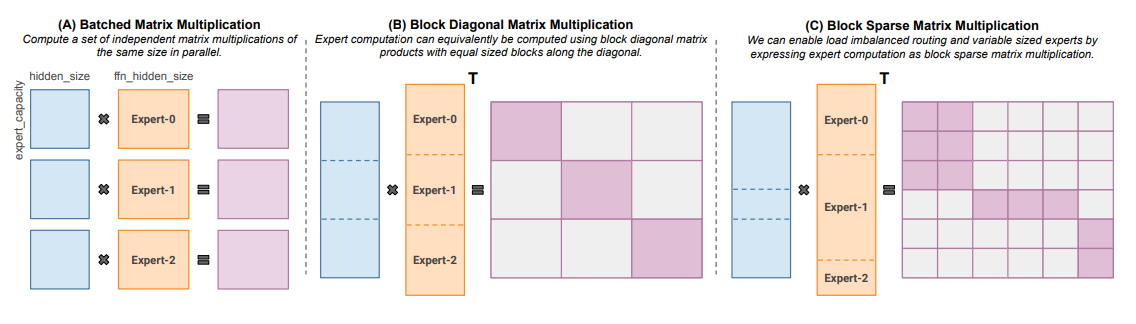
- Megablocks (Nov 2022) explores efficient sparse pretraining by providing new GPU kernels that can handle the dynamism present in MoEs. Their proposal never drops tokens and maps efficiently to modern hardware, leading to significant speedups. What’s the trick? Traditional MoEs use batched matrix multiplication, which assumes all experts have the same shape and the same number of tokens. In contrast, Megablocks expresses MoE layers as block-sparse operations that can accommodate imbalanced assignment.